Algebra - Hyperbolas

Show Mobile Notice Show All Notes Hide All Notes

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best views in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (should be able to scroll to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 4.4 : Hyperbolas

The next graph that we need to look at is the hyperbola. There are two basic forms of a hyperbola. Here are examples of each.

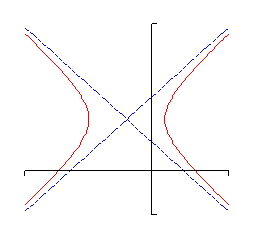
This graph does not have any tick marks on the x-axis or y-axis. There are two dashed line that intersect in the 2nd quadrant forming a giant “X”. In the left region of this “X” there is a graph that looks kind of like a parabola that has a vertex in the 1st quadrant and opens to the right. As the graph opens to the right it follows the two lines fairly closely. In the right region of the “X” there is another graph that looks like a parabola with vertex in the 2nd quadrant that opens to the left and as it opens to the left it follows the lines fairly closely.

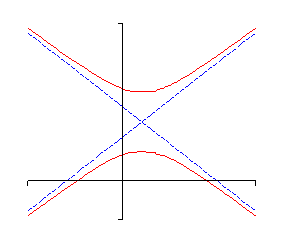
This graph does not have any tick marks on the x-axis or y-axis. There are two dashed line that intersect in the 1st quadrant forming a giant “X”. In the upper region of this “X” there is a graph that looks kind of like a parabola that has a vertex in the 1st quadrant and opens upwards. As the graph opens upwards it follows the two lines fairly closely. In the right region of the “X” there is another graph that looks like a parabola with vertex in the 1st quadrant that opens downwards and as it opens downwards it follows the lines fairly closely.

Hyperbolas consist of two vaguely parabola shaped pieces that open either up and down or right and left. Also, just like parabolas each of the pieces has a vertex. Note that they aren’t really parabolas, they just resemble parabolas.

There are also two lines on each graph. These lines are called asymptotes and as the graphs show as we make \(x\) large (in both the positive and negative sense) the graph of the hyperbola gets closer and closer to the asymptotes. The asymptotes are not officially part of the graph of the hyperbola. However, they are usually included so that we can make sure and get the sketch correct. The point where the two asymptotes cross is called the center of the hyperbola.

There are two standard forms of the hyperbola, one for each type shown above. Here is a table giving each form as well as the information we can get from each one.

Form	\(\displaystyle \frac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} - \frac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1\)	\(\displaystyle \frac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} - \frac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} = 1\)

Center	\(\left( {h,k} \right)\)	\(\left( {h,k} \right)\)

Opens	Opens left and right	Opens up and down

Vertices	\(\displaystyle \left( {h + a,k} \right)\) and \(\left( {h - a,k} \right)\)	\(\displaystyle \left( {h,k + b} \right)\) and \(\left( {h,k - b} \right)\)

Slope of Asymptotes	\(\displaystyle \pm \frac{b}{a}\)	\(\displaystyle \pm \frac{b}{a}\)

Equations of Asymptotes	\(\displaystyle y = k \pm \frac{b}{a}\left( {x - h} \right)\)	\(\displaystyle y = k \pm \frac{b}{a}\left( {x - h} \right)\)

Note that the difference between the two forms is which term has the minus sign. If the \(y\) term has the minus sign then the hyperbola will open left and right. If the \(x\) term has the minus sign then the hyperbola will open up and down.

We got the equations of the asymptotes by using the point-slope form of the line and the fact that we know that the asymptotes will go through the center of the hyperbola.

Let’s take a look at a couple of these.

Example 1 Sketch the graph of each of the following hyperbolas.

\(\displaystyle \frac{{{{\left( {x - 3} \right)}^2}}}{{25}} - \frac{{{{\left( {y + 1} \right)}^2}}}{{49}} = 1\)
\(\displaystyle \frac{{{y^2}}}{9} - {\left( {x + 2} \right)^2} = 1\)

Show All Solutions Hide All Solutions

a \(\displaystyle \frac{{{{\left( {x - 3} \right)}^2}}}{{25}} - \frac{{{{\left( {y + 1} \right)}^2}}}{{49}} = 1\) Show Solution

Now, notice that the \(y\) term has the minus sign and so we know that we’re in the first column of the table above and that the hyperbola will be opening left and right.

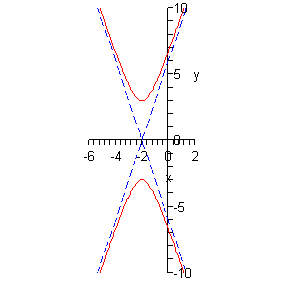
The first thing that we should get is the center since pretty much everything else is built around that. The center in this case is \(\left( {3, - 1} \right)\) and as always watch the signs! Once we have the center we can get the vertices. These are \(\left( {8, - 1} \right)\) and \(\left( { - 2, - 1} \right)\).

Next, we should get the slopes of the asymptotes. These are always the square root of the number under the \(y\) term divided by the square root of the number under the \(x\) term and there will always be a positive and a negative slope. The slopes are then \( \pm \frac{7}{5}\).

Now that we’ve got the center and the slopes of the asymptotes we can get the equations for the asymptotes. They are,

\[y = - 1 + \frac{7}{5}\left( {x - 3} \right)\hspace{0.25in}{\mbox{and}}\hspace{0.25in}y = - 1 - \frac{7}{5}\left( {x - 3} \right)\]

We can now start the sketching. We start by sketching the asymptotes and the vertices. Once these are done we know what the basic shape should look like so we sketch it in making sure that as \(x\) gets large we move in closer and closer to the asymptotes.

Here is the sketch for this hyperbola.

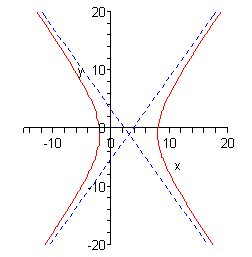
The domain of this graph is from -15 to 20 while the range is from -20 to 20. There are two dashed line that intersect at approximately (5,-1) forming a giant “X”. In the left region of this “X” there is a graph that looks kind of like a parabola that has a vertex at (8,-1) and opens to the right. As the graph opens to the right it follows the two lines fairly closely. In the right region of the “X” there is another graph that looks like a parabola with vertex at (-2,-1) that opens to the left and as it opens to the left it follows the lines fairly closely.

b \(\displaystyle \frac{{{y^2}}}{9} - {\left( {x + 2} \right)^2} = 1\) Show Solution

In this case the hyperbola will open up and down since the \(x\) term has the minus sign. Now, the center of this hyperbola is \(\left( { - 2,0} \right)\). Remember that since there is a y² term by itself we had to have \(k = 0\). At this point we also know that the vertices are \(\left( { - 2,3} \right)\) and \(\left( { - 2, - 3} \right)\).

In order to see the slopes of the asymptotes let’s rewrite the equation a little.

\[\frac{{{y^2}}}{9} - \frac{{{{\left( {x + 2} \right)}^2}}}{1} = 1\]

So, the slopes of the asymptotes are \( \pm \frac{3}{1} = \pm 3\). The equations of the asymptotes are then,

\[y = 0 + 3\left( {x + 2} \right) = 3x + 6\hspace{0.25in}{\mbox{and }}\hspace{0.25in}\,\,y = 0 - 3\left( {x + 2} \right) = - 3x - 6\]

Here is the sketch of this hyperbola.

The domain of this graph is from -6 to 2 while the range is from -10 to 10. There are two dashed line that intersect at (-2,0) forming a giant “X”. In the upper region of this “X” there is a graph that looks kind of like a parabola that has a vertex at (-2,3) and opens upward. As the graph opens upward it follows the two lines fairly closely. In the bottom region of the “X” there is another graph that looks like a parabola with vertex at (-2,-3) that opens downward and as it opens downward it follows the lines fairly closely.