Section 14.1 : Tangent Planes and Linear Approximations
Earlier we saw how the two partial derivatives \({f_x}\) and \({f_y}\) can be thought of as the slopes of traces. We want to extend this idea out a little in this section. The graph of a function \(z = f\left( {x,y} \right)\) is a surface in \({\mathbb{R}^3}\)(three dimensional space) and so we can now start thinking of the plane that is “tangent” to the surface as a point.
Let’s start out with a point \(\left( {{x_0},{y_0}} \right)\) and let’s let \({C_1}\) represent the trace to \(f\left( {x,y} \right)\) for the plane \(y = {y_0}\) (i.e. allowing \(x\) to vary with \(y\) held fixed) and we’ll let \({C_2}\) represent the trace to \(f\left( {x,y} \right)\) for the plane \(x = {x_0}\) (i.e. allowing \(y\) to vary with \(x\) held fixed). Now, we know that \({f_x}\left( {{x_0},{y_0}} \right)\) is the slope of the tangent line to the trace \({C_1}\) and \({f_y}\left( {{x_0},{y_0}} \right)\) is the slope of the tangent line to the trace \({C_2}\). So, let \({L_1}\) be the tangent line to the trace \({C_1}\) and let \({L_2}\) be the tangent line to the trace \({C_2}\).
The tangent plane will then be the plane that contains the two lines \({L_1}\) and \({L_2}\). Geometrically this plane will serve the same purpose that a tangent line did in Calculus I. A tangent line to a curve was a line that just touched the curve at that point and was “parallel” to the curve at the point in question. Well tangent planes to a surface are planes that just touch the surface at the point and are “parallel” to the surface at the point. Note that this gives us a point that is on the plane. Since the tangent plane and the surface touch at \(\left( {{x_0},{y_0}} \right)\) the following point will be on both the surface and the plane.
\[\left( {{x_0},{y_0},{z_0}} \right) = \left( {{x_0},{y_0},f\left( {{x_0},{y_0}} \right)} \right)\]What we need to do now is determine the equation of the tangent plane. We know that the general equation of a plane is given by,
\[a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) + c\left( {z - {z_0}} \right) = 0\]where \(\left( {{x_0},{y_0},{z_0}} \right)\) is a point that is on the plane, which we have. Let’s rewrite this a little. We’ll move the \(x\) terms and \(y\) terms to the other side and divide both sides by \(c\). Doing this gives,
\[z - {z_0} = - \frac{a}{c}\left( {x - {x_0}} \right) - \frac{b}{c}\left( {y - {y_0}} \right)\]Now, let’s rename the constants to simplify up the notation a little. Let’s rename them as follows,
\[A = - \frac{a}{c}\hspace{0.25in}B = - \frac{b}{c}\]With this renaming the equation of the tangent plane becomes,
\[z - {z_0} = A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right)\]and we need to determine values for \(A\) and \(B\).
Let’s first think about what happens if we hold \(y\) fixed, i.e. if we assume that \(y = {y_0}\). In this case the equation of the tangent plane becomes,
\[z - {z_0} = A\left( {x - {x_0}} \right)\]This is the equation of a line and this line must be tangent to the surface at \(\left( {{x_0},{y_0}} \right)\) (since it’s part of the tangent plane). In addition, this line assumes that \(y = {y_0}\) (i.e. fixed) and \(A\) is the slope of this line. But if we think about it this is exactly what the tangent to \({C_1}\) is, a line tangent to the surface at \(\left( {{x_0},{y_0}} \right)\) assuming that \(y = {y_0}\). In other words,
\[z - {z_0} = A\left( {x - {x_0}} \right)\]is the equation for \({L_1}\) and we know that the slope of \({L_1}\) is given by \({f_x}\left( {{x_0},{y_0}} \right)\). Therefore, we have the following,
\[A = {f_x}\left( {{x_0},{y_0}} \right)\]If we hold \(x\) fixed at \(x = {x_0}\) the equation of the tangent plane becomes,
\[z - {z_0} = B\left( {y - {y_0}} \right)\]However, by a similar argument to the one above we can see that this is nothing more than the equation for \({L_2}\) and that it’s slope is \(B\) or \({f_y}\left( {{x_0},{y_0}} \right)\). So,
\[B = {f_y}\left( {{x_0},{y_0}} \right)\]The equation of the tangent plane to the surface given by \(z = f\left( {x,y} \right)\) at \(\left( {{x_0},{y_0}} \right)\) is then,
\[z - {z_0} = {f_x}\left( {{x_0},{y_0}} \right)\left( {x - {x_0}} \right) + {f_y}\left( {{x_0},{y_0}} \right)\left( {y - {y_0}} \right)\]Also, if we use the fact that \({z_0} = f\left( {{x_0},{y_0}} \right)\) we can rewrite the equation of the tangent plane as,
\[\begin{align*}z - f\left( {{x_0},{y_0}} \right) & = {f_x}\left( {{x_0},{y_0}} \right)\left( {x - {x_0}} \right) + {f_y}\left( {{x_0},{y_0}} \right)\left( {y - {y_0}} \right)\\ z & = f\left( {{x_0},{y_0}} \right) + {f_x}\left( {{x_0},{y_0}} \right)\left( {x - {x_0}} \right) + {f_y}\left( {{x_0},{y_0}} \right)\left( {y - {y_0}} \right)\end{align*}\]We will see an easier derivation of this formula (actually a more general formula) in the next section so if you didn’t quite follow this argument hold off until then to see a better derivation.
There really isn’t too much to do here other than taking a couple of derivatives and doing some quick evaluations.
\[\begin{align*}f\left( {x,y} \right) & = \ln \left( {2x + y} \right)\hspace{0.25in}& {z_0}& = f\left( { - 1,3} \right) = \ln \left( 1 \right) = 0\\ {f_x}\left( {x,y} \right) & = \frac{2}{{2x + y}}\hspace{0.25in} &{f_x}\left( { - 1,3} \right) & = 2\\ {f_y}\left( {x,y} \right) & = \frac{1}{{2x + y}}\hspace{0.25in} & {f_y}\left( { - 1,3} \right) & = 1\end{align*}\]The equation of the plane is then,
\[\begin{align*}z - 0 & = 2\left( {x + 1} \right) + \left( 1 \right)\left( {y - 3} \right)\\ z & = 2x + y - 1\end{align*}\]One nice use of tangent planes is they give us a way to approximate a surface near a point. As long as we are near to the point \(\left( {{x_0},{y_0}} \right)\) then the tangent plane should nearly approximate the function at that point. Because of this we define the linear approximation to be,
\[L\left( {x,y} \right) = f\left( {{x_0},{y_0}} \right) + {f_x}\left( {{x_0},{y_0}} \right)\left( {x - {x_0}} \right) + {f_y}\left( {{x_0},{y_0}} \right)\left( {y - {y_0}} \right)\]and as long as we are “near” \(\left( {{x_0},{y_0}} \right)\) then we should have that,
\[f\left( {x,y} \right) \approx L\left( {x,y} \right) = f\left( {{x_0},{y_0}} \right) + {f_x}\left( {{x_0},{y_0}} \right)\left( {x - {x_0}} \right) + {f_y}\left( {{x_0},{y_0}} \right)\left( {y - {y_0}} \right)\]So, we’re really asking for the tangent plane so let’s find that.
\[\begin{align*}f\left( {x,y} \right) & = 3 + \frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9}\hspace{0.25in} & f\left( { - 4,3} \right) & = 3 + 1 + 1 = 5\\ {f_x}\left( {x,y} \right) & = \frac{x}{8}\hspace{0.25in} & {f_x}\left( { - 4,3} \right) & = - \frac{1}{2}\\ {f_y}\left( {x,y} \right) & = \frac{{2y}}{9}\hspace{0.25in} & {f_y}\left( { - 4,3} \right) & = \frac{2}{3}\end{align*}\]The tangent plane, or linear approximation, is then,
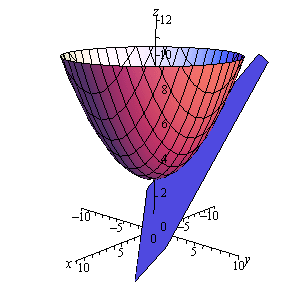
\[L\left( {x,y} \right) = 5 - \frac{1}{2}\left( {x + 4} \right) + \frac{2}{3}\left( {y - 3} \right)\]For reference purposes here is a sketch of the surface and the tangent plane/linear approximation.