Algebra - Transformations

Show Mobile Notice Show All Notes Hide All Notes

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best views in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (should be able to scroll to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 4.6 : Transformations

In this section we are going to see how knowledge of some fairly simple graphs can help us graph some more complicated graphs. Collectively the methods we’re going to be looking at in this section are called transformations.

Vertical Shifts

The first transformation we’ll look at is a vertical shift.

Given the graph of $f\left( x \right)$ the graph of $g\left( x \right) = f\left( x \right) + c$ will be the graph of $f\left( x \right)$ shifted up by $c$ units if $c$ is positive and or down by $c$ units if $c$ is negative.

So, if we can graph $f\left( x \right)$ getting the graph of $g\left( x \right)$ is fairly easy. Let’s take a look at a couple of examples.

Example 1 Using transformations sketch the graph of the following functions.

$g\left( x \right) = {x^2} + 3$
$f\left( x \right) = \sqrt x - 5$

Show All Solutions Hide All Solutions

Show Discussion

The first thing to do here is graph the function without the constant which by this point should be fairly simple for you. Then shift accordingly.

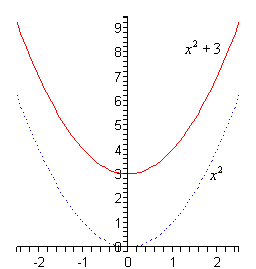
a $g\left( x \right) = {x^2} + 3$ Show Solution

In this case we first need to graph ${x^2}$ (the dotted line on the graph below) and then pick this up and shift it upwards by 3. Coordinate wise this will mean adding 3 onto all the $y$ coordinates of points on ${x^2}$.

Here is the sketch for this one.

$The domain of this graph is from -2.5 to 2.5 while the range is from 0 to 9.5. There are two functions graphed here. The graph of $x^{2}$ is graphed with a dotted line. You should be somewhat familiar with the graph of parabolas by know, but if not it looks vaguely like a “U” with its vertex at the origin and increases up into the 1st and 2nd quadrants as we move away from the y-axis in the positive and negative direction. The graph of $x^{2}+3$ is graphed with a solid line and is looks exactly like the graph of $x^{2}$ except the vertex is at the point (0,3). The graph still increases up into the 1st and 2nd quadrant as we move away from the y-axis.$

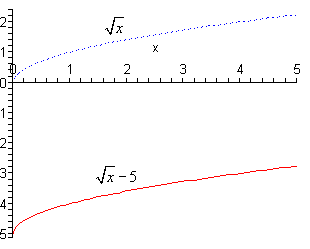
b $f\left( x \right) = \sqrt x - 5$ Show Solution

Okay, in this case we’re going to be shifting the graph of $\sqrt x $ (the dotted line on the graph below) down by 5. Again, from a coordinate standpoint this means that we subtract 5 from the $y$ coordinates of points on $\sqrt x $.

Here is this graph.

$The domain of this graph is from 0 to 5 while the range is from -5 to 2.5. There are two functions graphed here. The graph of $\sqrt{x}$ is graphed with a dotted line. You should be somewhat familiar with the graph of square roots by know, but if not it starts at the origin and increases fairly sharply out of the origin into the 1st quadrant between 0<x<0.2 or so and then bends over to the right with the rate of increase slowing down as it goes through the points (1,1) and (4,2). The graph of $\sqrt{x}-5$ is graphed with a solid line and is looks exactly like the graph of $\sqrt{x}$ except that is starts at (0,-5) instead. It increases sharply out of this point and then bends over to the right with a slowing of the rate of increase.$

So, vertical shifts aren’t all that bad if we can graph the “base” function first. Note as well that if you’re not sure that you believe the graphs in the previous set of examples all you need to do is plug a couple values of $x$ into the function and verify that they are in fact the correct graphs.

Horizontal Shifts

These are fairly simple as well although there is one bit where we need to be careful.

Given the graph of $f\left( x \right)$ the graph of $g\left( x \right) = f\left( {x + c} \right)$ will be the graph of $f\left( x \right)$ shifted left by $c$ units if $c$ is positive and or right by $c$ units if $c$ is negative.

Now, we need to be careful here. A positive $c$ shifts a graph in the negative direction and a negative $c$ shifts a graph in the positive direction. They are exactly opposite than vertical shifts and it’s easy to flip these around and shift incorrectly if we aren’t being careful.

Example 2 Using transformations sketch the graph of the following functions.

$h\left( x \right) = {\left( {x + 2} \right)^3}$
$g\left( x \right) = \sqrt {x - 4} $

Show All Solutions Hide All Solutions

a $h\left( x \right) = {\left( {x + 2} \right)^3}$ Show Solution

Okay, with these we need to first identify the “base” function. That is the function that’s being shifted. In this case it looks like we are shifting $f\left( x \right) = {x^3}$. We can then see that,

\[h\left( x \right) = {\left( {x + 2} \right)^3} = f\left( {x + 2} \right)\]

In this case $c = 2$ and so we’re going to shift the graph of $f\left( x \right) = {x^3}$ (the dotted line on the graph below) and move it 2 units to the left. This will mean subtracting 2 from the $x$ coordinates of all the points on $f\left( x \right) = {x^3}$.

Here is the graph for this problem.

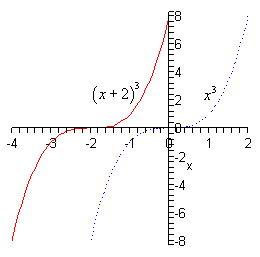
$The domain of this graph is from -4 to 2 while the range is from -8 to 8. There are two functions graphed here. The graph of $x^{3}$ is graphed with a dotted line. You should be somewhat familiar with the graph of cubics by know, but if not it starts at (-2,-8) and increases with a vaguely cupped downward curvature until it goes through the origin horizontally. As the graph moves into the 1st quadrant it continues to increase only it is now cupped vaguely upward as it increases until it ends at (2,8). The graph of $(x+2)^{3}$ is graphed with a solid line and is looks exactly like the graph of $x^{3}$ except that it is shifted over to the left by 2 units. So, it starts at (-4,8) and increases until it moves through the point (-2,0) horizontally and then continues to increase until ending at (0,8).$

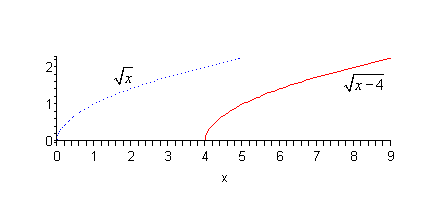
b $g\left( x \right) = \sqrt {x - 4} $ Show Solution

In this case it looks like the base function is $\sqrt x $ and it also looks like $c = - 4$ and so we will be shifting the graph of $\sqrt x $ (the dotted line on the graph below) to the right by 4 units. In terms of coordinates this will mean that we’re going to add 4 onto the $x$ coordinate of all the points on $\sqrt x $.

Here is the sketch for this function.

$The domain of this graph is from 0 to 5 while the range is from -5 to 2.5. There are two functions graphed here. The graph of $\sqrt{x}$ is graphed with a dotted line. You should be somewhat familiar with the graph of square roots by know, but if not it starts at the origin and increases fairly sharply out of the origin into the 1st quadrant between 0<x<0.2 or so and then bends over to the right with the rate of increase slowing down as it goes through the points (1,1) and (4,2). The graph of $\sqrt{x-4}$ is graphed with a solid line and is looks exactly like the graph of $\sqrt{x}$ except that it is shifted over 4 units to the right and starts at (4,0) instead. It increases sharply out of this point and then bends over to the right with a slowing of the rate of increase.$

Vertical and Horizontal Shifts

Now we can also combine the two shifts we just got done looking at into a single problem. If we know the graph of $f\left( x \right)$ the graph of $g\left( x \right) = f\left( {x + c} \right) + k$ will be the graph of $f\left( x \right)$ shifted left or right by $c$ units depending on the sign of $c$ and up or down by $k$ units depending on the sign of $k$.

Let’s take a look at a couple of examples.

Example 3 Use transformation to sketch the graph of each of the following.

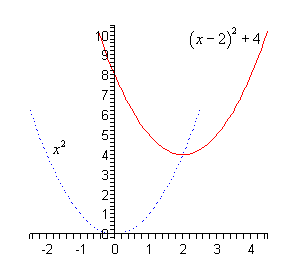
$f\left( x \right) = {\left( {x - 2} \right)^2} + 4$
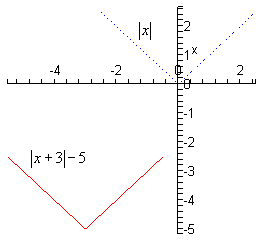
$g\left( x \right) = \left| {x + 3} \right| - 5$

Show All Solutions Hide All Solutions

a $f\left( x \right) = {\left( {x - 2} \right)^2} + 4$ Show Solution

In this part it looks like the base function is ${x^2}$ and it looks like will be shift this to the right by 2 (since $c = - 2$) and up by 4 (since $k = 4$). Here is the sketch of this function.

$The domain of this graph is from -2.5 to 4.5 while the range is from 0 to 10.5. There are two functions graphed here. The graph of $x^{2}$ is graphed with a dotted line. You should be somewhat familiar with the graph of parabolas by know, but if not it looks vaguely like a “U” with its vertex at the origin and increases up into the 1st and 2nd quadrants as we move away from the y-axis in the positive and negative direction. The graph of $(x-2)^{2}+4$ is graphed with a solid line and is looks exactly like the graph of $x^{2}$ except the vertex is at the point (2,4). The graph still increases upwards as it moves away from the vertex.$

b $g\left( x \right) = \left| {x + 3} \right| - 5$ Show Solution

For this part we will be shifting $\left| x \right|$ to the left by 3 (since $c = 3$) and down 5 (since $k = - 5$). Here is the sketch of this function.

The domain of this graph is from -5 to 2.5 while the range is from -5 to 2.5. There are two functions graphed here. The graph of $|x|$ is graphed with a dotted line. You should be somewhat familiar with the graph of absolute value by know, but if not it is a “V” that starts at the origin and moves up into the 1st and 2nd quadrant following the lines y=x and y=-x respectively. The graph of $|x+3|-5$ is graphed with a solid line and is looks exactly like the graph of $|x|$ except that the point of the “V” is now at (-3,-5) and it still increases up out of this point with lines that have slopes +1 (to the right of (-3,-5) ) and -1 (to the left of (-3,-5) ).

Reflections

The final set of transformations that we’re going to be looking at in this section aren’t shifts, but instead they are called reflections and there are two of them.

Reflection about the $x$-axis

Given the graph of $f\left( x \right)$ then the graph of $g\left( x \right) = - f\left( x \right)$ is the graph of $f\left( x \right)$ reflected about the $x$-axis. This means that the signs on the all the $y$ coordinates are changed to the opposite sign.

Reflection about the $y$-axis

Given the graph of $f\left( x \right)$ then the graph of $g\left( x \right) = f\left( { - x} \right)$ is the graph of $f\left( x \right)$ reflected about the $y$-axis. This means that the signs on the all the $x$ coordinates are changed to the opposite sign.

Here is an example of each.

Example 4 Using transformation sketch the graph of each of the following.

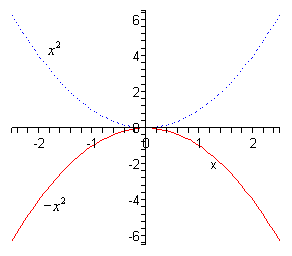
$g\left( x \right) = - {x^2}$
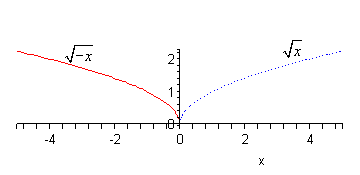
$h\left( x \right) = \sqrt { - x} $

Show All Solutions Hide All Solutions

a $g\left( x \right) = - {x^2}$ Show Solution

Based on the placement of the minus sign (i.e. it’s outside the square and NOT inside the square, or ${\left( { - x} \right)^2}$ ) it looks like we will be reflecting ${x^2}$ about the $x$-axis. So, again, the means that all we do is change the sign on all the $y$ coordinates.

Here is the sketch of this graph.

$The domain of this graph is from -2.5 to 4.5 while the range is from -6 to 6. There are two functions graphed here. The graph of $x^{2}$ is graphed with a dotted line. You should be somewhat familiar with the graph of parabolas by know, but if not it looks vaguely like a “U” with its vertex at the origin and increases up into the 1st and 2nd quadrants as we move away from the y-axis in the positive and negative direction. The graph of $-x^{2}$ is graphed with a solid line and is looks exactly like the graph of $x^{2}$ except that it is reflected about the x-axis and so while the vertex is still at the origin it now decreases out of the origin into the 3rd and 4th quadrants. Basically it looks like an upside down “U”.$

b $h\left( x \right) = \sqrt { - x} $ Show Solution

Now with this one let’s first address the minus sign under the square root in more general terms. We know that we can’t take the square roots of negative numbers, however the presence of that minus sign doesn’t necessarily cause problems. We won’t be able to plug positive values of $x$ into the function since that would give square roots of negative numbers. However, if $x$ were negative, then the negative of a negative number is positive and that is okay. For instance,

\[h\left( { - 4} \right) = \sqrt { - \left( { - 4} \right)} = \sqrt 4 = 2\]

So, don’t get all worried about that minus sign.

Now, let’s address the reflection here. Since the minus sign is under the square root as opposed to in front of it we are doing a reflection about the $y$-axis. This means that we’ll need to change all the signs of points on $\sqrt x $.

Note as well that this syncs up with our discussion on this minus sign at the start of this part.

Here is the graph for this function.

$The domain of this graph is from -5 to 5 while the range is from 0 to 2.5. There are two functions graphed here. The graph of $\sqrt{x}$ is graphed with a dotted line. You should be somewhat familiar with the graph of square roots by know, but if not it starts at the origin and increases fairly sharply out of the origin into the 1st quadrant between 0<x<0.2 or so and then bends over to the right with the rate of increase slowing down as it goes through the points (1,1) and (4,2). The graph of $\sqrt{-x}$ is graphed with a solid line and is looks exactly like the graph of $\sqrt{x}$ except that it is reflected about the y-axis. So, it still starts at (0,0) and it still increases fairly sharply out of the origin but it now increases into the 2nd quadrant rather than the 1st quadrant. After about x=-0.2 it bends over to the left and the rate of increase slows as it moves through the points (-1,1) and (-4,2).$

Section 4.6 : Transformations

Vertical Shifts

Horizontal Shifts

Vertical and Horizontal Shifts

Reflections

Reflection about the \(x\)-axis

Reflection about the \(y\)-axis