Section 9.8 : Area with Polar Coordinates
In this section we are going to look at areas enclosed by polar curves. Note as well that we said “enclosed by” instead of “under” as we typically have in these problems. These problems work a little differently in polar coordinates. Here is a sketch of what the area that we’ll be finding in this section looks like.
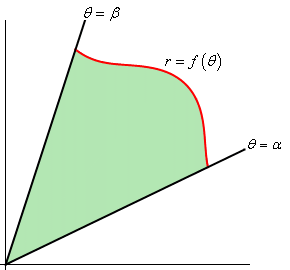
We’ll be looking for the shaded area in the sketch above. The formula for finding this area is,
Notice that we use \(r\) in the integral instead of \(f\left( \theta \right)\) so make sure and substitute accordingly when doing the integral.
Let’s take a look at an example.
We graphed this function back when we first started looking at polar coordinates. For this problem we’ll also need to know the values of \(\theta \) where the curve goes through the origin. We can get these by setting the equation equal to zero and solving.
\[\begin{align*}0 & = 2 + 4\cos \theta \\ \cos \theta & = - \frac{1}{2}\hspace{0.5in} \Rightarrow \hspace{0.5in}\theta = \frac{{2\pi }}{3},\frac{{4\pi }}{3}\end{align*}\]Here is the sketch of this curve with the inner loop shaded in.
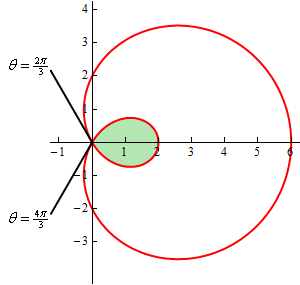
Can you see why we needed to know the values of \(\theta \) where the curve goes through the origin? These points define where the inner loop starts and ends and hence are also the limits of integration in the formula.
So, the area is then,
\[\begin{align*}A & = \int_{{\,\frac{{2\pi }}{3}}}^{{\,\frac{{4\pi }}{3}}}{{\frac{1}{2}{{\left( {2 + 4\cos \theta } \right)}^2}\,d\theta }}\\ & = \int_{{\,\frac{{2\pi }}{3}}}^{{\,\frac{{4\pi }}{3}}}{{\frac{1}{2}\left( {4 + 16\cos \theta + 16{{\cos }^2}\theta } \right)\,d\theta }}\\ & = \int_{{\,\frac{{2\pi }}{3}}}^{{\,\frac{{4\pi }}{3}}}{{2 + 8\cos \theta + 4\left( {1 + \cos \left( {2\theta } \right)} \right)\,d\theta }}\\ & = \int_{{\,\frac{{2\pi }}{3}}}^{{\,\frac{{4\pi }}{3}}}{{6 + 8\cos \theta + 4\cos \left( {2\theta } \right)\,d\theta }}\\ & = \left. {\left( {6\theta + 8\sin \theta + 2\sin \left( {2\theta } \right)} \right)} \right|_{\frac{{2\pi }}{3}}^{\frac{{4\pi }}{3}}\\ & = 4\pi - 6\sqrt 3 = 2.174\end{align*}\]You did follow the work done in this integral didn’t you? You’ll run into quite a few integrals of trig functions in this section so if you need to you should go back to the Integrals Involving Trig Functions sections and do a quick review.
So, that’s how we determine areas that are enclosed by a single curve, but what about situations like the following sketch where we want to find the area between two curves.
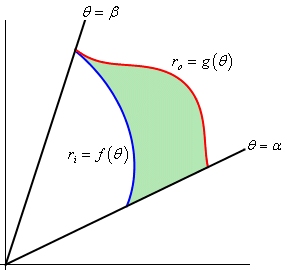
In this case we can use the above formula to find the area enclosed by both and then the actual area is the difference between the two. The formula for this is,
Let’s take a look at an example of this.
Here is a sketch of the region that we are after.
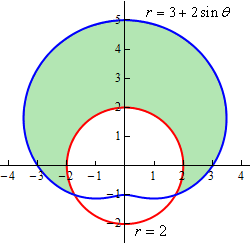
To determine this area, we’ll need to know the values of \(\theta \) for which the two curves intersect. We can determine these points by setting the two equations and solving.
\[\begin{align*}3 + 2\sin \theta & = 2\\ \sin \theta & = - \frac{1}{2}\hspace{0.5in} \Rightarrow \hspace{0.5in}\theta = \frac{{7\pi }}{6},\frac{{11\pi }}{6}\end{align*}\]Here is a sketch of the figure with these angles added.
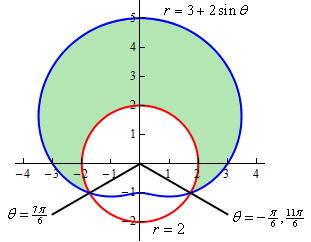
Note as well here that we also acknowledged that another representation for the angle \(\frac{{11\pi }}{6}\) is \( - \frac{\pi }{6}\). This is important for this problem. In order to use the formula above the area must be enclosed as we increase from the smaller to larger angle. So, if we use \(\frac{{7\pi }}{6}\) to \(\frac{{11\pi }}{6}\) we will not enclose the shaded area, instead we will enclose the bottom most of the three regions. However, if we use the angles \( - \frac{\pi }{6}\) to \(\frac{{7\pi }}{6}\) we will enclose the area that we’re after.
So, the area is then,
\[\begin{align*}A & = \int_{{\, - \frac{\pi }{6}}}^{{\,\frac{{7\pi }}{6}}}{{\frac{1}{2}\left( {{{\left( {3 + 2\sin \theta } \right)}^2} - {{\left( 2 \right)}^2}} \right)\,d\theta }}\\ & = \int_{{\, - \frac{\pi }{6}}}^{{\,\frac{{7\pi }}{6}}}{{\frac{1}{2}\left( {5 + 12\sin \theta + 4{{\sin }^2}\theta } \right)\,d\theta }}\\ & = \int_{{\, - \frac{\pi }{6}}}^{{\,\frac{{7\pi }}{6}}}{{\frac{1}{2}\left( {7 + 12\sin \theta - 2\cos \left( {2\theta } \right)} \right)\,d\theta }}\\ & = \left. {\frac{1}{2}\left( {7\theta - 12\cos \theta - \sin \left( {2\theta } \right)} \right)} \right|_{ - \frac{\pi }{6}}^{\frac{{7\pi }}{6}}\\ & = \frac{{11\sqrt 3 }}{2} + \frac{{14\pi }}{3} = 24.187\end{align*}\]Let’s work a slight modification of the previous example.
This time we’re looking for the following region.
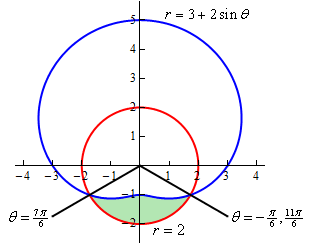
So, this is the region that we get by using the limits \(\frac{{7\pi }}{6}\) to \(\frac{{11\pi }}{6}\). The area for this region is,
\[\begin{align*}A & = \int_{{\,\frac{{7\pi }}{6}}}^{{\,\frac{{11\pi }}{6}}}{{\frac{1}{2}\left( {{{\left( 2 \right)}^2} - {{\left( {3 + 2\sin \theta } \right)}^2}} \right)\,d\theta }}\\ & = \int_{{\,\frac{{7\pi }}{6}}}^{{\,\frac{{11\pi }}{6}}}{{\frac{1}{2}\left( { - 5 - 12\sin \theta - 4{{\sin }^2}\theta } \right)\,d\theta }}\\ & = \int_{{\,\frac{{7\pi }}{6}}}^{{\,\frac{{11\pi }}{6}}}{{\frac{1}{2}\left( { - 7 - 12\sin \theta + 2\cos \left( {2\theta } \right)} \right)\,d\theta }}\\ & = \left. {\frac{1}{2}\left( { - 7\theta + 12\cos \theta + \sin \left( {2\theta } \right)} \right)} \right|_{\frac{{7\pi }}{6}}^{\frac{{11\pi }}{6}}\\ & = \frac{{11\sqrt 3 }}{2} - \frac{{7\pi }}{3} = 2.196\end{align*}\]Notice that for this area the “outer” and “inner” function were opposite!
Let’s do one final modification of this example.
Here is the sketch for this example.
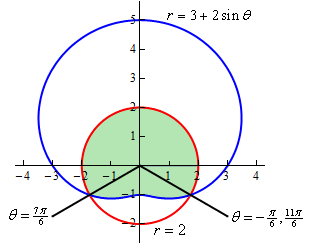
We are not going to be able to do this problem in the same fashion that we did the previous two. There is no set of limits that will allow us to enclose this area as we increase from one to the other. Remember that as we increase \(\theta \) the area we’re after must be enclosed. However, the only two ranges for \(\theta \) that we can work with enclose the area from the previous two examples and not this region.
In this case however, that is not a major problem. There are two ways to do get the area in this problem. We’ll take a look at both of them.
Solution 1
In this case let’s notice that the circle is divided up into two portions and we’re after the upper portion. Also notice that we found the area of the lower portion in Example 3. Therefore, the area is,
Solution 2
In this case we do pretty much the same thing except this time we’ll think of the area as the other portion of the limacon than the portion that we were dealing with in Example 2. We’ll also need to actually compute the area of the limacon in this case.
So, the area using this approach is then,
\[\begin{align*}{\mbox{Area}} & = {\mbox{Area of Limacon}} - {\mbox{Area from Example 2}}\\ & = \int_{{\,0}}^{{\,2\pi }}{{\frac{1}{2}{{\left( {3 + 2\sin \theta } \right)}^2}\,d\theta }} - 24.187\\ & = \int_{{\,0}}^{{\,2\pi }}{{\frac{1}{2}\left( {9 + 12\sin \theta + 4{{\sin }^2}\theta } \right)\,d\theta }} - 24.187\\ & = \int_{{\,0}}^{{\,2\pi }}{{\frac{1}{2}\left( {11 + 12\sin \theta - 2\cos \left( {2\theta } \right)} \right)\,d\theta }} - 24.187\\ & = \left. {\frac{1}{2}\left( {11\theta - 12\cos \left( \theta \right) - \sin \left( {2\theta } \right)} \right)} \right|_0^{2\pi } - 24.187\\ & = 11\pi - 24.187\\ & = 10.370\end{align*}\]A slightly longer approach, but sometimes we are forced to take this longer approach.
As this last example has shown we will not be able to get all areas in polar coordinates straight from an integral.