Section 4.1 : Rates of Change
The purpose of this section is to remind us of one of the more important applications of derivatives. That is the fact that \(f'\left( x \right)\) represents the rate of change of \(f\left( x \right)\). This is an application that we repeatedly saw in the previous chapter. Almost every section in the previous chapter contained at least one problem dealing with this application of derivatives. While this application will arise occasionally in this chapter we are going to focus more on other applications in this chapter.
So, to make sure that we don’t forget about this application here is a brief set of examples concentrating on the rate of change application of derivatives. Note that the point of these examples is to remind you of material covered in the previous chapter and not to teach you how to do these kinds of problems. If you don’t recall how to do these kinds of examples you’ll need to go back and review the previous chapter.
First, we’ll need to take the derivative of the function.
\[g'\left( x \right) = - 6 + 20\sin \left( {2x} \right)\]
Now, the function will not be changing if the rate of change is zero and so to answer this question we need to determine where the derivative is zero. So, let’s set this equal to zero and solve.
\[ - 6 + 20\sin \left( {2x} \right) = 0\hspace{0.5in} \Rightarrow \hspace{0.5in}\sin \left( {2x} \right) = \frac{6}{{20}} = 0.3\]
The solution to this is then,
\[\begin{alignat}{4}2x = & 0.3047 + 2\pi n & & \hspace{0.5in}\,\,\,\,{\mbox{OR}}\hspace{0.5in}\,\,\,\, & 2x = & 2.8369 + 2\pi n & & \hspace{0.25in}n = 0, \pm 1, \pm 2, \ldots \\ x = & 0.1524 + \pi n & & \hspace{0.5in}\,\,\,\,{\mbox{OR}}\hspace{0.5in}\,\,\, & x = & 1.4185 + \pi n & & \hspace{0.25in}n = 0, \pm 1, \pm 2, \ldots \end{alignat}\]
If you don’t recall how to solve trig equations check out the Solving Trig Equations sections in the Review Chapter.
As with the first problem we first need to take the derivative of the function.
\[A'\left( t \right) = 135{t^4} - 180{t^3} - 390{t^2} = 15{t^2}\left( {9{t^2} - 12t - 26} \right)\]
Next, we need to determine where the function isn’t changing. This is at,
\[\begin{align*}t & = 0\\ t & = \frac{{12 \pm \sqrt {144 - 4\left( 9 \right)\left( { - 26} \right)} }}{{18}} = \frac{{12 \pm \sqrt {1080} }}{{18}} = \frac{{12 \pm 6\sqrt {30} }}{{18}} = \frac{{2 \pm \sqrt {30} }}{3} = - 1.159,\,\,\,\,2.492\end{align*}\]
So, the function is not changing at three values of \(t\). Finally, to determine where the function is increasing or decreasing we need to determine where the derivative is positive or negative. Recall that if the derivative is positive then the function must be increasing and if the derivative is negative then the function must be decreasing. The following number line gives this information.
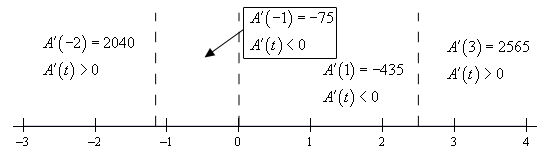
So, from this number line we can see that we have the following increasing and decreasing information.
\[{\mbox{Increasing :}}\,\, - \infty < t < - 1.159,\,\,\,2.492 < t < \infty \,\,\,\,\,\,\,\,{\mbox{Decreasing :}} - 1.159 < t < 0,\,\,\,0 < t < 2.492\]
If you don’t remember how to solve polynomial and rational inequalities then you should check out the appropriate sections in the Review Chapter.
Finally, we can’t forget about Related Rates problems.
The first thing to do here is to get sketch a figure showing the situation.
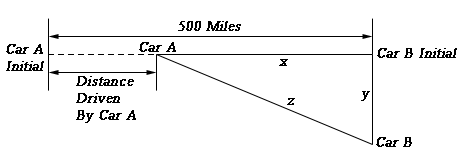
In this figure \(y\) represents the distance driven by Car B and \(x\) represents the distance separating Car A from Car B’s initial position and \(z\) represents the distance separating the two cars. After 3 hours driving time with have the following values of \(x\) and \(y\).
\[x = 500 - 35\left( 3 \right) = 395\hspace{0.5in}\hspace{0.25in}y = 50\left( 3 \right) = 150\]
We can use the Pythagorean theorem to find \(z\) at this time as follows,
\[{z^2} = {395^2} + {150^2} = 178525\hspace{0.5in} \Rightarrow \hspace{0.5in}z = \sqrt {178525} = 422.5222\]
Now, to answer this question we will need to determine \(z'\) given that \(x' = - 35\) and \(y' = 50\). Do you agree with the signs on the two given rates? Remember that a rate is negative if the quantity is decreasing and positive if the quantity is increasing.
We can again use the Pythagorean theorem here. First, write it down and the remember that \(x\), \(y\), and \(z\) are all changing with time and so differentiate the equation using Implicit Differentiation.
\[{z^2} = {x^2} + {y^2}\hspace{0.5in} \Rightarrow \hspace{0.5in}2zz' = 2xx' + 2yy'\]
Finally, all we need to do is cancel a two from everything, plug in for the known quantities and solve for \(z'\).
\[z'\left( {422.5222} \right) = \left( {395} \right)\left( { - 35} \right) + \left( {150} \right)\left( {50} \right)\hspace{0.25in} \Rightarrow \hspace{0.5in}z' = \frac{{ - 6325}}{{422.5222}} = - 14.9696\]
So, after three hours the distance between them is decreasing at a rate of 14.9696 mph.
So, in this section we covered three “standard” problems using the idea that the derivative of a function gives the rate of change of the function. As mentioned earlier, this chapter will be focusing more on other applications than the idea of rate of change, however, we can’t forget this application as it is a very important one.