Section 17.5 : Stokes' Theorem
In this section we are going to take a look at a theorem that is a higher dimensional version of Green’s Theorem. In Green’s Theorem we related a line integral to a double integral over some region. In this section we are going to relate a line integral to a surface integral. However, before we give the theorem we first need to define the curve that we’re going to use in the line integral.
Let’s start off with the following surface with the indicated orientation.
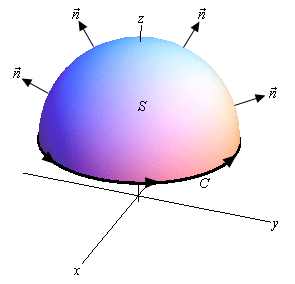
Around the edge of this surface we have a curve \(C\). This curve is called the boundary curve. The orientation of the surface \(S\) will induce the positive orientation of \(C\). To get the positive orientation of \(C\) think of yourself as walking along the curve. While you are walking along the curve if your head is pointing in the same direction as the unit normal vectors while the surface is on the left then you are walking in the positive direction on \(C\).
Now that we have this curve definition out of the way we can give Stokes’ Theorem.
Stokes’ Theorem
Let \(S\) be an oriented smooth surface that is bounded by a simple, closed, smooth boundary curve \(C\) with positive orientation. Also let \(\vec F\) be a vector field then,
\[\int\limits_{C}{{\vec F\centerdot \,d\,\vec r}} = \iint\limits_{S}{{{\mathop{\rm curl}\nolimits} \vec F\,\centerdot \,d\vec S}}\]In this theorem note that the surface \(S\) can actually be any surface so long as its boundary curve is given by \(C\). This is something that can be used to our advantage to simplify the surface integral on occasion.
Let’s take a look at a couple of examples.
Let’s start this off with a sketch of the surface.
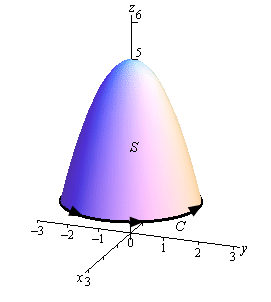
In this case the boundary curve \(C\) will be where the surface intersects the plane \(z = 1\) and so will be the curve
\[\begin{align*}1 & = 5 - {x^2} - {y^2}\\ {x^2} + {y^2} & = 4\hspace{0.25in}{\mbox{at }}z = 1\end{align*}\]So, the boundary curve will be the circle of radius 2 that is in the plane \(z = 1\). The parameterization of this curve is,
\[\vec r\left( t \right) = 2\cos t\,\vec i + 2\sin t\,\vec j + \vec k,\,\,\,\,0 \le t \le 2\pi \]The first two components give the circle and the third component makes sure that it is in the plane \(z = 1\).
Using Stokes’ Theorem we can write the surface integral as the following line integral.
\[\iint\limits_{S}{{{\mathop{\rm curl}\nolimits} \vec F\,\centerdot \,d\vec S}} = \int\limits_{C}{{\vec F\,\centerdot \,d\,\vec r}} = \int_{{\,0}}^{{\,2\pi }}{{\vec F\left( {\vec r\left( t \right)} \right)\,\centerdot \,\vec r'\left( t \right)\,dt}}\]So, it looks like we need a couple of quantities before we do this integral. Let’s first get the vector field evaluated on the curve. Remember that this is simply plugging the components of the parameterization into the vector field.
\[\begin{align*}\vec F\left( {\vec r\left( t \right)} \right) & = {\left( 1 \right)^2}\,\vec i - 3\left( {2\cos t} \right)\left( {2\sin t} \right)\,\vec j + {\left( {2\cos t} \right)^3}{\left( {2\sin t} \right)^3}\,\vec k\\ & = \vec i - 12\cos t\sin t\,\vec j + 64{\cos ^3}t{\sin ^3}t\,\vec k\end{align*}\]Next, we need the derivative of the parameterization and the dot product of this and the vector field.
\[\begin{align*}\vec r'\left( t \right) & = - 2\sin t\,\vec i + 2\cos t\,\vec j\\ \vec F\left( {\vec r\left( t \right)} \right)\,\centerdot \,\vec r'\left( t \right)\, & = - 2\sin t - 24\sin t{\cos ^2}t\end{align*}\]We can now do the integral.
\[\begin{align*}\iint\limits_{S}{{{\mathop{\rm curl}\nolimits} \vec F\,\centerdot \,d\vec S}} & = \int_{{\,0}}^{{\,2\pi }}{{ - 2\sin t - 24\sin t{{\cos }^2}t\,dt}}\\ & = \left. {\left( {2\cos t + 8{{\cos }^3}t} \right)} \right|_0^{2\pi }\\ & = 0\end{align*}\]We are going to need the curl of the vector field eventually so let’s get that out of the way first.
\[{\mathop{\rm curl}\nolimits} \vec F = \left| {\begin{array}{*{20}{c}}{\vec i}&{\vec j}&{\vec k}\\{\frac{\partial }{{\partial x}}}&{\frac{\partial }{{\partial y}}}&{\frac{\partial }{{\partial z}}}\\{{z^2}}&{{y^2}}&x\end{array}} \right| = 2z\,\vec j - \vec j = \left( {2z - 1} \right)\vec j\]Now, all we have is the boundary curve for the surface that we’ll need to use in the surface integral. However, as noted above all we need is any surface that has this as its boundary curve. So, let’s use the following plane with upwards orientation for the surface.
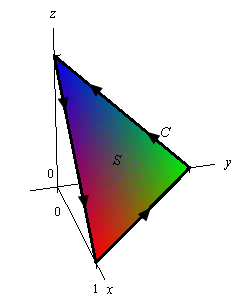
Since the plane is oriented upwards this induces the positive direction on \(C\) as shown. The equation of this plane is,
\[x + y + z = 1\hspace{0.25in}\,\,\, \Rightarrow \hspace{0.25in}\,\,\,z = g\left( {x,y} \right) = 1 - x - y\]Now, let’s use Stokes’ Theorem and get the surface integral set up.
\[\begin{align*}\int\limits_{C}{{\vec F\,\centerdot \,d\,\vec r}} & = \iint\limits_{S}{{{\mathop{\rm curl}\nolimits} \vec F\,\centerdot \,d\vec S}}\\ & = \iint\limits_{S}{{\left( {2z - 1} \right)\vec j\centerdot d\vec S}}\\ & = \iint\limits_{D}{{\left( {2z - 1} \right)\vec j\centerdot \frac{{\nabla f}}{{\left\| {\nabla f} \right\|}}\,\,\left\| {\nabla f} \right\|\,dA}}\end{align*}\]Okay, we now need to find a couple of quantities. First let’s get the gradient. Recall that this comes from the function of the surface.
\[\begin{align*}f\left( {x,y,z} \right) &= z - g\left( {x,y} \right) = z - 1 + x + y\\ & \nabla f = \vec i + \vec j + \vec k\end{align*}\]Note as well that this also points upwards and so we have the correct direction.
Now, \(D\) is the region in the \(xy\)-plane shown below,
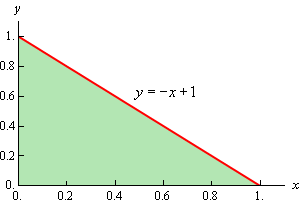
We get the equation of the line by plugging in \(z = 0\) into the equation of the plane. So based on this the ranges that define \(D\) are,
\[0 \le x \le 1\hspace{0.25in}0 \le y \le - x + 1\]The integral is then,
\[\begin{align*}\int\limits_{C}{{\vec F\,\centerdot \,d\,\vec r}} & = \iint\limits_{D}{{\left( {2z - 1} \right)\vec j\centerdot \left( {\vec i + \vec j + \vec k} \right)\,dA}}\\ & = \int_{{\,0}}^{{\,1}}{{\int_{{\,0}}^{{ - x + 1}}{{2\left( {1 - x - y} \right) - 1\,dy}}\,dx}}\end{align*}\]Don’t forget to plug in for \(z\) since we are doing the surface integral on the plane. Finishing this out gives,
\[\begin{align*}\int\limits_{C}{{\vec F\,\centerdot \,d\,\vec r}} & = \int_{{\,0}}^{{\,1}}{{\int_{{\,0}}^{{ - x + 1}}{{1 - 2x - 2y\,dy}}\,dx}}\\ & = \int_{{\,0}}^{{\,1}}{{\left. {\left( {y - 2xy - {y^2}} \right)} \right|_0^{ - x + 1}\,dx}}\\ & = \int_{{\,0}}^{{\,1}}{{{x^2} - x\,dx}}\\ & = \left. {\left( {\frac{1}{3}{x^3} - \frac{1}{2}{x^2}} \right)} \right|_0^1\\ & = - \frac{1}{6}\end{align*}\]In both of these examples we were able to take an integral that would have been somewhat unpleasant to deal with and by the use of Stokes’ Theorem we were able to convert it into an integral that wasn’t too bad.