There’s really not a whole lot to do in solving this kind of trig equation. We first need to get the trig function on one side by itself. To do this all we need to do is divide both sides by 2.

\[\begin{align*}2\cos \left( t \right) & = \sqrt 3 \\ \cos \left( t \right) & = \frac{{\sqrt 3 }}{2}\end{align*}\]

We are looking for all the values of \(t\) for which cosine will have the value of \(\frac{{\sqrt 3 }}{2}\). So, let’s take a look at the following unit circle.

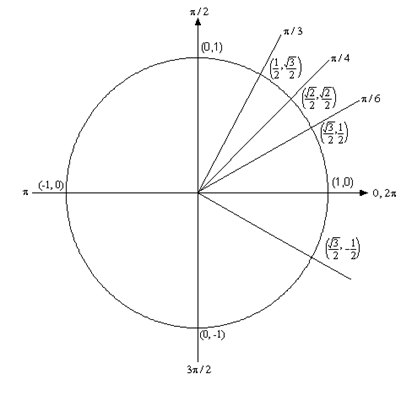
From quick inspection we can see that \(t = \frac{\pi }{6}\) is a solution. However, as we have shown on the unit circle there is another angle which will also be a solution. We need to determine what this angle is. When we look for these angles we typically want positive angles that lie between 0 and \(2\pi \). This angle will not be the only possibility of course, but we typically look for angles that meet these conditions.

To find this angle for this problem all we need to do is use a little geometry. The angle in the first quadrant makes an angle of \(\frac{\pi }{6}\) with the positive \(x\)-axis, then so must the angle in the fourth quadrant. So, we have two options. We could use \( - \frac{\pi }{6}\), but again, it’s more common to use positive angles. To get a positive angle all we need to do is use the fact that the angle is \(\frac{\pi }{6}\) with the positive \(x\)-axis (as noted above) and a positive angle will be \(t = 2\pi - \frac{\pi }{6} = \frac{{11\pi }}{6}\).

One way to remember how to get the positive form of the second angle is to think of making one full revolution from the positive \(x\)-axis (i.e. \(2\pi \)) and then backing off (i.e. subtracting) \(\frac{\pi }{6}\).

We aren’t done with this problem. As the discussion about finding the second angle has shown there are many ways to write any given angle on the unit circle. Sometimes it will be \( - \frac{\pi }{6}\) that we want for the solution and sometimes we will want both (or neither) of the listed angles. Therefore, since there isn’t anything in this problem (contrast this with the next problem) to tell us which is the correct solution we will need to list ALL possible solutions.

This is very easy to do. Recall from the previous section and you’ll see there that we used

\[\frac{\pi }{6} + 2\pi \,n\,,\;\;n = 0,\, \pm 1,\, \pm 2,\, \pm 3,\, \ldots \]

to represent all the possible angles that can end at the same location on the unit circle, i.e. angles that end at \(\frac{\pi }{6}\). Remember that all this says is that we start at \(\frac{\pi }{6}\) then rotate around in the counter-clockwise direction (\(n\) is positive) or clockwise direction (\(n\) is negative) for \(n\) complete rotations. The same thing can be done for the second solution.

So, all together the complete solution to this problem is

\[\begin{gather*}\frac{\pi }{6} + 2\pi \,n\,,\;\;n = 0,\, \pm 1,\, \pm 2,\, \pm 3,\, \ldots \\ \frac{{11\pi }}{6} + 2\pi \,n\,,\;\;n = 0,\, \pm 1,\, \pm 2,\, \pm 3,\, \ldots \end{gather*}\]

As a final thought, notice that we can get \( - \frac{\pi }{6}\) by using \(n = - 1\) in the second solution.

In a calculus class we are often more interested in only the solutions to a trig equation that fall in a certain interval. The first step in this kind of problem is to find all possible solutions. We did this in the previous example.

\[\begin{gather*}\frac{\pi }{6} + 2\pi \,n\,,\;\;n = 0,\, \pm 1,\, \pm 2,\, \pm 3,\, \ldots \\ \frac{{11\pi }}{6} + 2\pi \,n\,,\;\;n = 0,\, \pm 1,\, \pm 2,\, \pm 3,\, \ldots \end{gather*}\]

Now, to find the solutions in the interval all we need to do is start picking values of \(n\), plugging them in and getting the solutions that will fall into the interval that we’ve been given.

\(n=0\). \[\begin{align*}& \frac{\pi }{6} + 2\pi \,\left( 0 \right)\, = \frac{\pi }{6} < 2\pi \\ &\frac{{11\pi }}{6} + 2\pi \,\left( 0 \right) = \frac{{11\pi }}{6} < 2\pi \end{align*}\]

Now, notice that if we take any positive value of \(n\) we will be adding on positive multiples of \(2\pi \) onto a positive quantity and this will take us past the upper bound of our interval so we don’t need to take any positive value of \(n\).

However, just because we aren’t going to take any positive value of \(n\) doesn’t mean that we shouldn’t also look at negative values of \(n\).

\(n=-1\). \[\begin{align*}& \frac{\pi }{6} + 2\pi \,\left( { - 1} \right)\, = - \frac{{11\pi }}{6} > - 2\pi \\ & \frac{{11\pi }}{6} + 2\pi \,\left( { - 1} \right) = - \frac{\pi }{6} > - 2\pi \end{align*}\]

These are both greater than \( - 2\pi \)and so are solutions, but if we subtract another \(2\pi \) off (i.e use \(n = - 2\)) we will once again be outside of the interval so we’ve found all the possible solutions that lie inside the interval \([ - 2\pi ,2\pi ]\).

So, the solutions are : \(\frac{\pi }{6},\;\frac{{11\pi }}{6},\; - \frac{\pi }{6},\; - \frac{{11\pi }}{6}\).

This problem is very similar to the other problems in this section with a very important difference. We’ll start this problem in exactly the same way as we did in the first example. So, first get the sine on one side by itself.

\[\begin{align*}2\sin (5x) & = - \sqrt 3 \\ \sin (5x) & = \frac{{ - \sqrt 3 }}{2}\end{align*}\]

We are looking for angles that will give \( - \frac{{\sqrt 3 }}{2}\) out of the sine function. Let’s again go to our trusty unit circle.

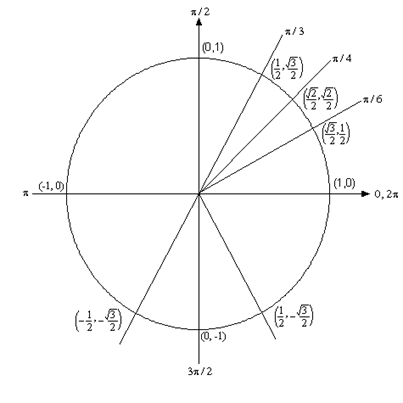
Now, there are no angles in the first quadrant for which sine has a value of \( - \frac{{\sqrt 3 }}{2}\). However, there are two angles in the lower half of the unit circle for which sine will have a value of \( - \frac{{\sqrt 3 }}{2}\). So, what are these angles?

Notice that \(\sin \left( {\frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2}\). Given this we now know that the angle in the third quadrant will be \(\frac{\pi }{3}\) below the negative \(x\)-axis or \(\pi + \frac{\pi }{3} = \frac{{4\pi }}{3}\). An easy way to remember this is to notice that we’ll rotate half a revolution from the positive \(x\)-axis to get to the negative \(x\)-axis then add on \(\frac{\pi }{3}\) to reach the angle we are looking for.

Likewise, the angle in the fourth quadrant will \(\frac{\pi }{3}\) below the positive \(x\)-axis. So, we could use \( - \frac{\pi }{3}\) or \(2\pi - \frac{\pi }{3} = \frac{{5\pi }}{3}\). Remember that we’re typically looking for positive angles between 0 and \(2\pi \) so we’ll use the positive angle. An easy way to remember how to the positive angle here is to rotate one full revolution from the positive \(x\)-axis (i.e. \(2\pi \)) and then backing off (i.e. subtracting) \(\frac{\pi }{3}\).

Now we come to the very important difference between this problem and the previous problems in this section. The solution is NOT

\[\begin{align*}x & = \frac{{4\pi }}{3} + 2\pi n,\quad n = 0, \pm 1, \pm 2, \ldots \\ x & = \frac{{5\pi }}{3} + 2\pi n,\quad n = 0, \pm 1, \pm 2, \ldots \end{align*}\]

This is not the set of solutions because we are NOT looking for values of \(x\) for which \(\sin \left( x \right) = - \frac{{\sqrt 3 }}{2}\), but instead we are looking for values of \(x\) for which \(\sin \left( {5x} \right) = - \frac{{\sqrt 3 }}{2}\). Note the difference in the arguments of the sine function! One is \(x\) and the other is \(5x\). This makes all the difference in the world in finding the solution! Therefore, the set of solutions is

\[\begin{align*}5x & = \frac{{4\pi }}{3} + 2\pi n,\quad n = 0, \pm 1, \pm 2, \ldots \\ 5x & = \frac{{5\pi }}{3} + 2\pi n,\quad n = 0, \pm 1, \pm 2, \ldots \end{align*}\]

Well, actually, that’s not quite the solution. We are looking for values of \(x\) so divide everything by 5 to get.

\[\begin{align*}x & = \frac{{4\pi }}{{15}} + \frac{{2\pi n}}{5},\quad n = 0, \pm 1, \pm 2, \ldots \\ x & = \frac{\pi }{3} + \frac{{2\pi n}}{5},\quad n = 0, \pm 1, \pm 2, \ldots \end{align*}\]

Notice that we also divided the \(2\pi n\)by 5 as well! This is important! If we don’t do that you WILL miss solutions. For instance, take \(n = 1\).

\[\begin{align*}x & = \frac{{4\pi }}{{15}} + \frac{{2\pi }}{5} = \frac{{10\pi }}{{15}} = \frac{{2\pi }}{3} & \hspace{0.25in} & \Rightarrow \hspace{0.5in}\sin \left( {5\left( {\frac{{2\pi }}{3}} \right)} \right) = \sin \left( {\frac{{10\pi }}{3}} \right) = - \frac{{\sqrt 3 }}{2}\\ x & = \frac{\pi }{3} + \frac{{2\pi }}{5} = \frac{{11\pi }}{{15}} & \hspace{0.25in} & \Rightarrow \hspace{0.5in}\sin \left( {5\left( {\frac{{11\pi }}{{15}}} \right)} \right) = \sin \left( {\frac{{11\pi }}{3}} \right) = - \frac{{\sqrt 3 }}{2}\end{align*}\]

We’ll leave it to you to verify our work showing they are solutions. However, it makes the point. If you didn’t divide the \(2\pi n\) by 5 you would have missed these solutions!

Okay, now that we’ve gotten all possible solutions it’s time to find the solutions on the given interval. We’ll do this as we did in the previous problem. Pick values of \(n\) and get the solutions.

\(n = 0\). \[\begin{align*}x & = \frac{{4\pi }}{{15}} + \frac{{2\pi \left( 0 \right)}}{5} = \frac{{4\pi }}{{15}} < 2\pi \\ x & = \frac{\pi }{3} + \frac{{2\pi \left( 0 \right)}}{5} = \frac{\pi }{3} < 2\pi \end{align*}\] \(n = 1\). \[\begin{align*}x & = \frac{{4\pi }}{{15}} + \frac{{2\pi \left( 1 \right)}}{5} = \frac{{2\pi }}{3} < 2\pi \\ x & = \frac{\pi }{3} + \frac{{2\pi \left( 1 \right)}}{5} = \frac{{11\pi }}{{15}} < 2\pi \end{align*}\] \(n = 2\). \[\begin{align*}x & = \frac{{4\pi }}{{15}} + \frac{{2\pi \left( 2 \right)}}{5} = \frac{{16\pi }}{{15}} < 2\pi \\ x & = \frac{\pi }{3} + \frac{{2\pi \left( 2 \right)}}{5} = \frac{{17\pi }}{{15}} < 2\pi \end{align*}\] \(n = 3\). \[\begin{align*}x & = \frac{{4\pi }}{{15}} + \frac{{2\pi \left( 3 \right)}}{5} = \frac{{22\pi }}{{15}} < 2\pi \\ x & = \frac{\pi }{3} + \frac{{2\pi \left( 3 \right)}}{5} = \frac{{23\pi }}{{15}} < 2\pi \end{align*}\] \(n = 4\). \[\begin{align*}x & = \frac{{4\pi }}{{15}} + \frac{{2\pi \left( 4 \right)}}{5} = \frac{{28\pi }}{{15}} < 2\pi \\ x & = \frac{\pi }{3} + \frac{{2\pi \left( 4 \right)}}{5} = \frac{{29\pi }}{{15}} < 2\pi \end{align*}\] \(n = 5\). \[\begin{align*}x & = \frac{{4\pi }}{{15}} + \frac{{2\pi \left( 5 \right)}}{5} = \frac{{34\pi }}{{15}} > 2\pi \\ x & = \frac{\pi }{3} + \frac{{2\pi \left( 5 \right)}}{5} = \frac{{35\pi }}{{15}} > 2\pi \end{align*}\]

Okay, so we finally got past the right endpoint of our interval so we don’t need any more positive n. Now let’s take a look at the negative \(n\) and see what we’ve got.

\(n = ­­–1 \). \[\begin{align*}x & = \frac{{4\pi }}{{15}} + \frac{{2\pi \left( { - 1} \right)}}{5} = - \frac{{2\pi }}{{15}} > - \pi \\ x & = \frac{\pi }{3} + \frac{{2\pi \left( { - 1} \right)}}{5} = - \frac{\pi }{{15}} > - \pi \end{align*}\] \(n = ­­–2\). \[\begin{align*}x & = \frac{{4\pi }}{{15}} + \frac{{2\pi \left( { - 2} \right)}}{5} = - \frac{{8\pi }}{{15}} > - \pi \\ x & = \frac{\pi }{3} + \frac{{2\pi \left( { - 2} \right)}}{5} = - \frac{{7\pi }}{{15}} > - \pi \end{align*}\] \(n = ­­–3\). \[\begin{align*}x & = \frac{{4\pi }}{{15}} + \frac{{2\pi \left( { - 3} \right)}}{5} = - \frac{{14\pi }}{{15}} > - \pi \\ x & = \frac{\pi }{3} + \frac{{2\pi \left( { - 3} \right)}}{5} = - \frac{{13\pi }}{{15}} > - \pi \end{align*}\] \(n = ­­–4\). \[\begin{align*}x & = \frac{{4\pi }}{{15}} + \frac{{2\pi \left( { - 4} \right)}}{5} = - \frac{{4\pi }}{3} < - \pi \\ x & = \frac{\pi }{3} + \frac{{2\pi \left( { - 4} \right)}}{5} = - \frac{{19\pi }}{{15}} < - \pi \end{align*}\]

And we’re now past the left endpoint of the interval. Sometimes, there will be many solutions as there were in this example. Putting all of this together gives the following set of solutions that lie in the given interval.

\[\begin{align*} & \frac{{4\pi }}{{15}},\frac{\pi }{3},\frac{{2\pi }}{3},\frac{{11\pi }}{{15}},\frac{{16\pi }}{{15}},\frac{{17\pi }}{{15}},\frac{{22\pi }}{{15}},\frac{{23\pi }}{{15}},\frac{{28\pi }}{{15}},\frac{{29\pi }}{{15}}\\ & - \frac{\pi }{{15}}, - \frac{{2\pi }}{{15}}, - \frac{{7\pi }}{{15}}, - \frac{{8\pi }}{{15}}, - \frac{{13\pi }}{{15}}, - \frac{{14\pi }}{{15}}\end{align*}\]

This problem is a little different from the previous ones. First, we need to do some rearranging and simplification.

\[\begin{align*}\sin (2x) & = - \cos (2x)\\ \frac{{\sin (2x)}}{{\cos (2x)}} & = - 1\\ \tan \left( {2x} \right) & = - 1\end{align*}\]

So, solving \(\sin (2x) = - \cos (2x)\) is the same as solving \(\tan (2x) = - 1\). Hopefully, you’ll recall that the smallest positive angle where tangent it -1 is \(\frac{{3\pi }}{4}\) and this angle is in the 2^nd quadrant.

There is also a second angle for which tangent will be -1 and we can use the unit circle to illustrate this second angle. Let’s take a look at the following unit circle.

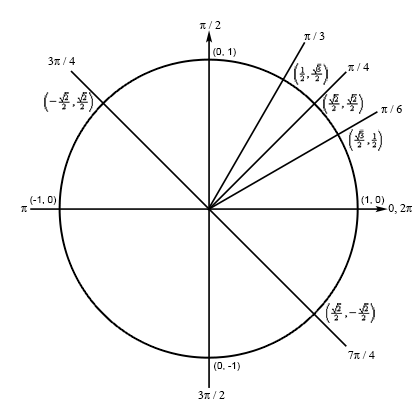
As shown in this unit circle if we add \(\pi \) to our first angle we get \(\frac{{3\pi }}{4} + \pi = \frac{{7\pi }}{4}\) and we get an angle that is in the fourth quadrant and has the same coordinates except for opposite signs. This means that tangent will also have a value of -1 here and so is a second angle.

This will always be true when solving tangent equations. Once we have one angle that will solve the equation a second angle will always be \(\pi \) plus the first angle.

All possible angles are then,

\[\begin{align*}2x & = \frac{{3\pi }}{4} + 2\pi n,\quad n = 0, \pm 1, \pm 2, \ldots \\ 2x & = \frac{{7\pi }}{4} + 2\pi n,\quad n = 0, \pm 1, \pm 2, \ldots \end{align*}\]

Or, upon dividing by the 2 we get all possible solutions.

\[\begin{align*}x & = \frac{{3\pi }}{8} + \pi n,\quad n = 0, \pm 1, \pm 2, \ldots \\ x & = \frac{{7\pi }}{8} + \pi n,\quad n = 0, \pm 1, \pm 2, \ldots \end{align*}\]

Now, let’s determine the solutions that lie in the given interval.

\(n = 0\). \[\begin{align*}x & = \frac{{3\pi }}{8} + \pi \left( 0 \right) = \frac{{3\pi }}{8} < \frac{{3\pi }}{2}\\ x & = \frac{{7\pi }}{8} + \pi \left( 0 \right) = \frac{{7\pi }}{8} < \frac{{3\pi }}{2}\end{align*}\] \(n = 1\). \[\begin{align*}x & = \frac{{3\pi }}{8} + \pi \left( 1 \right) = \frac{{11\pi }}{8} < \frac{{3\pi }}{2}\\ x & = \frac{{7\pi }}{8} + \pi \left( 1 \right) = \frac{{15\pi }}{8} > \frac{{3\pi }}{2}\end{align*}\]

Unlike the previous example only one of these will be in the interval. This will happen occasionally so don’t always expect both answers from a particular \(n\) to work. Also, we should now check \(n=2\) for the first to see if it will be in or out of the interval. I’ll leave it to you to check that it’s out of the interval.

Now, let’s check the negative \(n\).

\(n = ­­–1\). \[\begin{align*}x & = \frac{{3\pi }}{8} + \pi \left( { - 1} \right) = - \frac{{5\pi }}{8} > - \frac{{3\pi }}{2}\\ x & = \frac{{7\pi }}{8} + \pi \left( { - 1} \right) = - \frac{\pi }{8} > - \frac{{3\pi }}{2}\end{align*}\] \(n = ­­–2\). \[\begin{align*}x & = \frac{{3\pi }}{8} + \pi \left( { - 2} \right) = - \frac{{13\pi }}{8} < - \frac{{3\pi }}{2}\\ x & = \frac{{7\pi }}{8} + \pi \left( { - 2} \right) = - \frac{{9\pi }}{8} > - \frac{{3\pi }}{2}\end{align*}\]

Again, only one will work here. I’ll leave it to you to verify that \(n = ­­–3\) will give two answers that are both out of the interval.

The complete list of solutions is then,

\[ - \frac{{9\pi }}{8}, - \frac{{5\pi }}{8}, - \frac{\pi }{8},\frac{{3\pi }}{8},\frac{{7\pi }}{8},\frac{{11\pi }}{8}\]

This example is designed to remind you of certain properties about sine and cosine. Recall that \( - 1 \le \cos \left( \theta \right) \le 1\) and \( - 1 \le \sin \left( \theta \right) \le 1\). Therefore, since cosine will never be greater that 1 it definitely can’t be 2. So THERE ARE NO SOLUTIONS to this equation!

It is important to remember that not all trig equations will have solutions.