Section 15.9 : Surface Area
In this section we will look at the lone application (aside from the area and volume interpretations) of multiple integrals in this material. This is not the first time that we’ve looked at surface area We first saw surface area in Calculus II, however, in that setting we were looking at the surface area of a solid of revolution. In other words, we were looking at the surface area of a solid obtained by rotating a function about the \(x\) or \(y\) axis. In this section we want to look at a much more general setting although you will note that the formula here is very similar to the formula we saw back in Calculus II.
Here we want to find the surface area of the surface given by \(z = f\left( {x,y} \right)\) where \(\left( {x,y} \right)\) is a point from the region \(D\) in the \(xy\)-plane. In this case the surface area is given by,
Let’s take a look at a couple of examples.
Remember that the first octant is the portion of the xyz-axis system in which all three variables are positive. Let’s first get a sketch of the part of the plane that we are interested in.
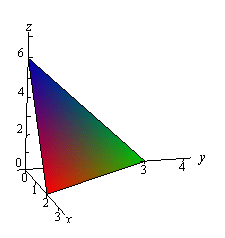
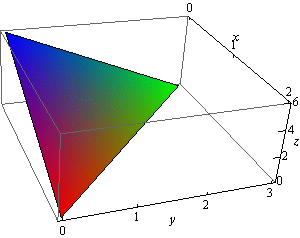
We’ll also need a sketch of the region \(D\).
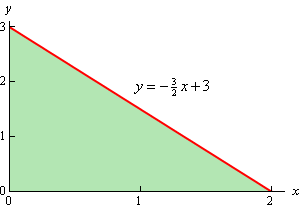
Remember that to get the region \(D\) we can pretend that we are standing directly over the plane and what we see is the region \(D\). We can get the equation for the hypotenuse of the triangle by realizing that this is nothing more than the line where the plane intersects the \(xy\)-plane and we also know that \(z = 0\) on the \(xy\)-plane. Plugging \(z = 0\) into the equation of the plane will give us the equation for the hypotenuse.
Notice that in order to use the surface area formula we need to have the function in the form \(z = f\left( {x,y} \right)\) and so solving for \(z\) and taking the partial derivatives gives,
\[z = 6 - 3x - 2y\hspace{0.5in}{f_x} = - 3\hspace{0.25in}{f_y} = - 2\]The limits defining \(D\) are,
\[0 \le x \le 2\hspace{0.5in}0 \le y \le - \frac{3}{2}x + 3\]The surface area is then,
\[\begin{align*}S & = \iint\limits_{D}{{\sqrt {\,{{\left[ { - 3} \right]}^2} + {{\left[ { - 2} \right]}^2} + 1} \,dA}}\\ & = \int_{{\,0}}^{{\,2}}{{\int_{{\,0}}^{{\, - \frac{3}{2}x + 3}}{{\sqrt {14} \,dy}}\,dx}}\\ & = \sqrt {14} \int_{{\,0}}^{{\,2}}{{ - \frac{3}{2}x + 3\,dx}}\\ & = \sqrt {14} \left. {\left( { - \frac{3}{4}{x^2} + 3x} \right)} \right|_0^2\\ & = 3\sqrt {14} \end{align*}\]In this case we are looking for the surface area of the part of \(z = xy\) where \(\left( {x,y} \right)\) comes from the disk of radius 1 centered at the origin since that is the region that will lie inside the given cylinder.
Here are the partial derivatives,
\[{f_x} = y\hspace{0.5in}{f_y} = x\]The integral for the surface area is,
\[S = \iint\limits_{D}{{\sqrt {\,{x^2} + {y^2} + 1} \,dA}}\]Given that \(D\) is a disk it makes sense to do this integral in polar coordinates.
\[\begin{align*}S & = \iint\limits_{D}{{\sqrt {\,{x^2} + {y^2} + 1} \,dA}}\\ & = \int_{{\,0}}^{{\,2\pi }}{{\int_{{\,0}}^{{\,1}}{{r\sqrt {1 + {r^2}} \,dr}}\,d\theta }}\\ & = \int_{{\,0}}^{{\,2\pi }}{{\left. {\frac{1}{2}\left( {\frac{2}{3}} \right){{\left( {1 + {r^2}} \right)}^{\frac{3}{2}}}} \right|_0^1\,d\theta }}\\ & = \int_{{\,0}}^{{\,2\pi }}{{\frac{1}{3}\left( {{2^{\frac{3}{2}}} - 1} \right)\,d\theta }}\\ & = \frac{{2\pi }}{3}\left( {{2^{\frac{3}{2}}} - 1} \right)\end{align*}\]