Algebra - Inverse Functions

Show Mobile Notice Show All Notes Hide All Notes

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 3.7 : Inverse Functions

In the last example from the previous section we looked at the two functions $f\left( x \right) = 3x - 2$ and $g\left( x \right) = \frac{x}{3} + \frac{2}{3}$ and saw that

\[\left( {f \circ g} \right)\left( x \right) = \left( {g \circ f} \right)\left( x \right) = x\]

and as noted in that section this means that these are very special functions. Let’s see just what makes them so special. Consider the following evaluations.

\[\require{color} \begin{align*}f\left( {\color{ProcessBlue} - 1} \right) & = 3\left( { - 1} \right) - 2 = {\color{Red} - 5} & \hspace{0.25in} \Rightarrow \hspace{0.25in}g\left( {\color{Red} - 5} \right) & = \frac{{ - 5}}{3} + \frac{2}{3} = \frac{{ - 3}}{3} = {\color{ProcessBlue} - 1}\\ & & \\ g\left( {\color{ProcessBlue} 2} \right) & = \frac{2}{3} + \frac{2}{3} = { \color{Red}\frac{4}{3}} & \hspace{0.25in} \Rightarrow \hspace{0.25in}f\left( {\color{Red} \frac{4}{3}} \right) & = 3\left( {\frac{4}{3}} \right) - 2 = 4 - 2 = {\color{ProcessBlue} 2 }\end{align*}\]

In the first case we plugged $x = - 1$ into $f\left( x \right)$ and got a value of -5. We then turned around and plugged $x = - 5$ into $g\left( x \right)$ and got a value of -1, the number that we started off with.

In the second case we did something similar. Here we plugged $x = 2$ into $g\left( x \right)$ and got a value of$\frac{4}{3}$, we turned around and plugged this into $f\left( x \right)$ and got a value of 2, which is again the number that we started with.

Note that we really are doing some function composition here. The first case is really,

\[\left( {g \circ f} \right)\left( { - 1} \right) = g\left[ {f\left( { - 1} \right)} \right] = g\left[ { - 5} \right] = - 1\]

and the second case is really,

\[\left( {f \circ g} \right)\left( 2 \right) = f\left[ {g\left( 2 \right)} \right] = f\left[ {\frac{4}{3}} \right] = 2\]

Note as well that these both agree with the formula for the compositions that we found in the previous section. We get back out of the function evaluation the number that we originally plugged into the composition.

So, just what is going on here? In some way we can think of these two functions as undoing what the other did to a number. In the first case we plugged $x = - 1$ into $f\left( x \right)$ and then plugged the result from this function evaluation back into $g\left( x \right)$ and in some way $g\left( x \right)$ undid what $f\left( x \right)$ had done to $x = - 1$ and gave us back the original $x$ that we started with.

Function pairs that exhibit this behavior are called inverse functions. Before formally defining inverse functions and the notation that we’re going to use for them we need to get a definition out of the way.

A function is called one-to-one if no two values of $x$ produce the same $y$. This is a fairly simple definition of one-to-one but it takes an example of a function that isn’t one-to-one to show just what it means. Before doing that however we should note that this definition of one-to-one is not really the mathematically correct definition of one-to-one. It is identical to the mathematically correct definition it just doesn’t use all the notation from the formal definition.

Now, let’s see an example of a function that isn’t one-to-one. The function $f\left( x \right) = {x^2}$ is not one-to-one because both $f\left( { - 2} \right) = 4$ and $f\left( 2 \right) = 4$. In other words, there are two different values of $x$ that produce the same value of $y$. Note that we can turn $f\left( x \right) = {x^2}$ into a one-to-one function if we restrict ourselves to $0 \le x < \infty $. This can sometimes be done with functions.

Showing that a function is one-to-one is often a tedious and difficult process. For the most part we are going to assume that the functions that we’re going to be dealing with in this section are one-to-one. We did need to talk about one-to-one functions however since only one-to-one functions can be inverse functions.

Now, let’s formally define just what inverse functions are.

Inverse Functions

Given two one-to-one functions $f\left( x \right)$ and $g\left( x \right)$ if

\[\left( {f \circ g} \right)\left( x \right) = x\hspace{0.25in}\hspace{0.25in}{\mbox{AND}}\hspace{0.25in}\hspace{0.25in}\left( {g \circ f} \right)\left( x \right) = x\]

then we say that $f\left( x \right)$ and $g\left( x \right)$ are inverses of each other. More specifically we will say that $g\left( x \right)$ is the inverse of $f\left( x \right)$ and denote it by

\[g\left( x \right) = {f^{ - 1}}\left( x \right)\]

Likewise, we could also say that $f\left( x \right)$ is the inverse of $g\left( x \right)$ and denote it by

\[f\left( x \right) = {g^{ - 1}}\left( x \right)\]

The notation that we use really depends upon the problem. In most cases either is acceptable.

For the two functions that we started off this section with we could write either of the following two sets of notation.

\[\begin{align*}f\left( x \right) & = 3x - 2 & \hspace{0.25in}\hspace{0.25in}{f^{ - 1}}\left( x \right) & = \frac{x}{3} + \frac{2}{3}\\ & \\ g\left( x \right) & = \frac{x}{3} + \frac{2}{3} &\hspace{0.25in}\hspace{0.25in}{g^{ - 1}}\left( x \right) & = 3x - 2\end{align*}\]

Now, be careful with the notation for inverses. The “-1” is NOT an exponent despite the fact that it sure does look like one! When dealing with inverse functions we’ve got to remember that

\[{f^{ - 1}}\left( x \right) \ne \frac{1}{{f\left( x \right)}}\]

This is one of the more common mistakes that students make when first studying inverse functions.

The process for finding the inverse of a function is a fairly simple one although there is a couple of steps that can on occasion be somewhat messy. Here is the process

Finding the Inverse of a Function

Given the function $f\left( x \right)$ we want to find the inverse function, ${f^{ - 1}}\left( x \right)$.

First, replace $f\left( x \right)$ with $y$. This is done to make the rest of the process easier.
Replace every $x$ with a $y$ and replace every $y$ with an $x$.
Solve the equation from Step 2 for $y$. This is the step where mistakes are most often made so be careful with this step.
Replace $y$ with ${f^{ - 1}}\left( x \right)$. In other words, we’ve managed to find the inverse at this point!
Verify your work by checking that $\left( {f \circ {f^{ - 1}}} \right)\left( x \right) = x$ and $\left( {{f^{ - 1}} \circ f} \right)\left( x \right) = x$ are both true. This work can sometimes be messy making it easy to make mistakes so again be careful.

That’s the process. Most of the steps are not all that bad but as mentioned in the process there are a couple of steps that we really need to be careful with.

In the verification step we technically really do need to check that both $\left( {f \circ {f^{ - 1}}} \right)\left( x \right) = x$ and $\left( {{f^{ - 1}} \circ f} \right)\left( x \right) = x$ are true. For all the functions that we are going to be looking at in this section if one is true then the other will also be true. However, there are functions (they are far beyond the scope of this course however) for which it is possible for only one of these to be true. This is brought up because in all the problems here we will be just checking one of them. We just need to always remember that technically we should check both.

Let’s work some examples.

Example 1 Given $f\left( x \right) = 3x - 2$ find ${f^{ - 1}}\left( x \right)$.

Show Solution

Now, we already know what the inverse to this function is as we’ve already done some work with it. However, it would be nice to actually start with this since we know what we should get. This will work as a nice verification of the process.

So, let’s get started. We’ll first replace $f\left( x \right)$ with $y$.

\[y = 3x - 2\]

Next, replace all $x$’s with $y$ and all y’s with $x$.

\[x = 3y - 2\]

Now, solve for $y$.

\[\begin{align*}x + 2 & = 3y\\ \frac{1}{3}\left( {x + 2} \right) & = y\\ \frac{x}{3} + \frac{2}{3} & = y\end{align*}\]

Finally replace $y$ with ${f^{ - 1}}\left( x \right)$.

\[{f^{ - 1}}\left( x \right) = \frac{x}{3} + \frac{2}{3}\]

Now, we need to verify the results. We already took care of this in the previous section, however, we really should follow the process so we’ll do that here. It doesn’t matter which of the two that we check we just need to check one of them. This time we’ll check that $\left( {f \circ {f^{ - 1}}} \right)\left( x \right) = x$ is true.

\[\begin{align*}\left( {f \circ {f^{ - 1}}} \right)\left( x \right) & = f\left[ {{f^{ - 1}}\left( x \right)} \right]\\ & = f\left[ {\frac{x}{3} + \frac{2}{3}} \right]\\ & = 3\left( {\frac{x}{3} + \frac{2}{3}} \right) - 2\\ & = x + 2 - 2\\ & = x\end{align*}\]

Example 2 Given $g\left( x \right) = \sqrt {x - 3} $ find ${g^{ - 1}}\left( x \right)$, $x \ge 0$.

Show Solution

Now the fact that we’re now using $g\left( x \right)$ instead of $f\left( x \right)$ doesn’t change how the process works. Here are the first few steps.

\[\begin{align*}y & = \sqrt {x - 3} \\ x & = \sqrt {y - 3} \end{align*}\]

Now, to solve for $y$ we will need to first square both sides and then proceed as normal.

\[\begin{align*}x & = \sqrt {y - 3} \\ {x^2} & = y - 3\\ {x^2} + 3 & = y\end{align*}\]

This inverse is then,

\[{g^{ - 1}}\left( x \right) = {x^2} + 3\]

Finally let’s verify and this time we’ll use the other one just so we can say that we’ve gotten both down somewhere in an example.

\[\begin{align*}\left( {{g^{ - 1}} \circ g} \right)\left( x \right) & = {g^{ - 1}}\left[ {g\left( x \right)} \right]\\ & = {g^{ - 1}}\left( {\sqrt {x - 3} } \right)\\ & = {\left( {\sqrt {x - 3} } \right)^2} + 3\\ & = x - 3 + 3\\ & = x\end{align*}\]

So, we did the work correctly and we do indeed have the inverse.

Before we move on we should also acknowledge the restrictions of $x \ge 0$ that we gave in the problem statement but never apparently did anything with. Note that this restriction is required to make sure that the inverse, ${g^{ - 1}}\left( x \right)$ given above is in fact one-to-one.

Without this restriction the inverse would not be one-to-one as is easily seen by a couple of quick evaluations.

\[{g^{ - 1}}\left( 1 \right) = {\left( 1 \right)^2} + 3 = 4\hspace{0.25in}\hspace{0.25in}\hspace{0.25in}{g^{ - 1}}\left( { - 1} \right) = {\left( { - 1} \right)^2} + 3 = 4\]

Therefore, the restriction is required in order to make sure the inverse is one-to-one.

The next example can be a little messy so be careful with the work here.

Example 3 Given $h\left( x \right) = \frac{{x + 4}}{{2x - 5}}$ find ${h^{ - 1}}\left( x \right)$.

Show Solution

The first couple of steps are pretty much the same as the previous examples so here they are,

\[\begin{align*}y & = \frac{{x + 4}}{{2x - 5}}\\ x & = \frac{{y + 4}}{{2y - 5}}\end{align*}\]

Now, be careful with the solution step. With this kind of problem it is very easy to make a mistake here.

\[\begin{align*}x\left( {2y - 5} \right) & = y + 4\\ 2xy - 5x & = y + 4\\ 2xy - y & = 4 + 5x\\ \left( {2x - 1} \right)y & = 4 + 5x\\ y & = \frac{{4 + 5x}}{{2x - 1}}\end{align*}\]

So, if we’ve done all of our work correctly the inverse should be,

\[{h^{ - 1}}\left( x \right) = \frac{{4 + 5x}}{{2x - 1}}\]

Finally, we’ll need to do the verification. This is also a fairly messy process and it doesn’t really matter which one we work with.

\[\begin{align*}\left( {h \circ {h^{ - 1}}} \right)\left( x \right) & = h\left[ {{h^{ - 1}}\left( x \right)} \right]\\ & = h\left[ {\frac{{4 + 5x}}{{2x - 1}}} \right]\\ & = \frac{{\frac{{4 + 5x}}{{2x - 1}} + 4}}{{2\left( {\frac{{4 + 5x}}{{2x - 1}}} \right) - 5}}\end{align*}\]

Okay, this is a mess. Let’s simplify things up a little bit by multiplying the numerator and denominator by $2x - 1$.

\[\begin{align*}\left( {h \circ {h^{ - 1}}} \right)\left( x \right) & = \frac{{2x - 1}}{{2x - 1}}\,\,\frac{{\frac{{4 + 5x}}{{2x - 1}} + 4}}{{2\left( {\frac{{4 + 5x}}{{2x - 1}}} \right) - 5}}\\ & = \frac{{\left( {2x - 1} \right)\left( {\frac{{4 + 5x}}{{2x - 1}} + 4} \right)}}{{\left( {2x - 1} \right)\left( {2\left( {\frac{{4 + 5x}}{{2x - 1}}} \right) - 5} \right)}}\\ & = \frac{{4 + 5x + 4\left( {2x - 1} \right)}}{{2\left( {4 + 5x} \right) - 5\left( {2x - 1} \right)}}\\ & = \frac{{4 + 5x + 8x - 4}}{{8 + 10x - 10x + 5}}\\ & = \frac{{13x}}{{13}}\\ & = x\end{align*}\]

Wow. That was a lot of work, but it all worked out in the end. We did all of our work correctly and we do in fact have the inverse.

There is one final topic that we need to address quickly before we leave this section. There is an interesting relationship between the graph of a function and its inverse.

Here is the graph of the function and inverse from the first two examples. We’ll not deal with the final example since that is a function that we haven’t really talked about graphing yet.

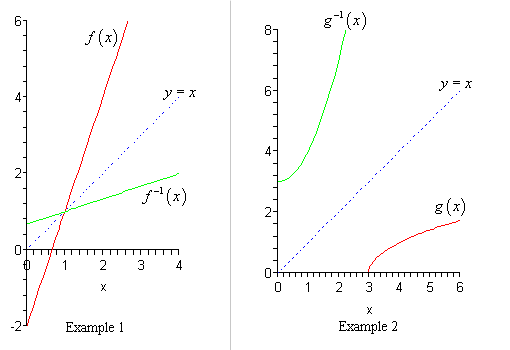
$There are two graphs in this image. The graph on the left is labeled “Example 1” and the domain is from 0 to 4 while the range is from -2 to 6. There is a dotted line going through the points (0,0) and (1,1) labeled “y=x”. There is also a line going through the points (0,-2) and (1,1) that is labeled $f(x)$. Finally, there is a line going through the points (0,2/3) and (1,1) and is labeled $f^{-1}(x)$. All three lines intersect at (1,1) and the line labeled $f^{-1}(x)$ appears to be a reflecting of the line $f(x)$ about the line y=x. The graph on the right is labeled “Example 2” and the domain is from 0 to 6 while the range is from 0 to 8. There is a dotted line going through the points (0,0) and (1,1) labeled “y=x”. There is a graph starting at (3,0) and increasing as it moves to the right. It is also bending over so that the rate of increase lessens as x increases. This graph is labeled $g(x)$. There is also a graph starting at (0,3) and initially moves to the right with a slight increase before bending upwards into a steep increase as x increases. This graph is labeled $g^{-1}(x)$. The graph labeled $g^{-1}(x)$ appears to be a reflecting of the graph $g(x)$ about the line y=x.$

In both cases we can see that the graph of the inverse is a reflection of the actual function about the line $y = x$. This will always be the case with the graphs of a function and its inverse.