Section 8.4 : Hydrostatic Pressure and Force
In this section we are going to submerge a vertical plate in water and we want to know the force that is exerted on the plate due to the pressure of the water. This force is often called the hydrostatic force.
There are two basic formulas that we’ll be using here. First, if we are \(d\) meters below the surface then the hydrostatic pressure is given by,
\[P = \rho gd\]where, \(\rho \) is the density of the fluid and \(g\) is the gravitational acceleration. We are going to assume that the fluid in question is water and since we are going to be using the metric system these quantities become,
\[\rho = 1000{\mbox{ kg/}}{{\mbox{m}}^{\mbox{3}}}\hspace{0.25in}\hspace{0.25in}g = 9.81{\mbox{ m/}}{{\mbox{s}}^{\mbox{2}}}\]The second formula that we need is the following. Assume that a constant pressure \(P\) is acting on a surface with area \(A\). Then the hydrostatic force that acts on the area is,
\[F = PA\]Note that we won’t be able to find the hydrostatic force on a vertical plate using this formula since the pressure will vary with depth and hence will not be constant as required by this formula. We will however need this for our work.
The best way to see how these problems work is to do an example or two.
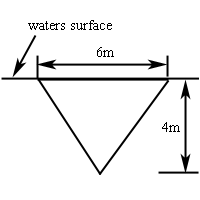
The first thing to do here is set up an axis system. So, let’s redo the sketch above with the following axis system added in.
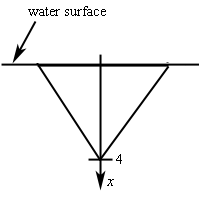
So, we are going to orient the \(x\)-axis so that positive \(x\) is downward, \(x = 0\) corresponds to the water surface and \(x = 4\) corresponds to the depth of the tip of the triangle.
Next we break up the triangle into \(n\) horizontal strips each of equal width \(\Delta x\) and in each interval \(\left[ {{x_{i - 1}},{x_i}} \right]\) choose any point \(x_i^*\). In order to make the computations easier we are going to make two assumptions about these strips. First, we will ignore the fact that the ends are actually going to be slanted and assume the strips are rectangular. If \(\Delta x\) is sufficiently small this will not affect our computations much. Second, we will assume that \(\Delta x\) is small enough that the hydrostatic pressure on each strip is essentially constant.
Below is a representative strip.
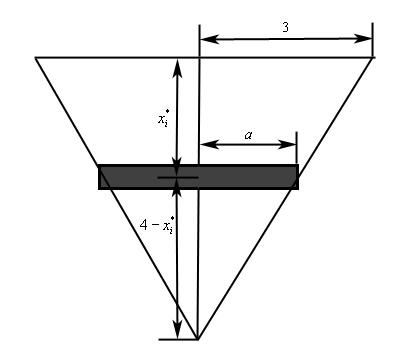
The height of this strip is \(\Delta x\) and the width is 2\(a\). We can use similar triangles to determine \(a\) as follows,
\[\frac{3}{4} = \frac{a}{{4 - x_i^*}}\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}a = 3 - \frac{3}{4}x_i^*\]Now, since we are assuming the pressure on this strip is constant, the pressure is given by,
\[{P_i} = \rho gd = 1000\left( {9.81} \right)x_i^* = 9810x_i^*\]and the hydrostatic force on each strip is,
\[{F_i} = {P_i}\,A = {P_i}\left( {2a\Delta x} \right) = 9810x_i^*\left( 2 \right)\left( {3 - \frac{3}{4}x_i^*} \right)\Delta x = 19620x_i^*\left( {3 - \frac{3}{4}x_i^*} \right)\,\Delta x\]The approximate hydrostatic force on the plate is then the sum of the forces on all the strips or,
\[F \approx \sum\limits_{i = 1}^n {19620x_i^*\left( {3 - \frac{3}{4}x_i^*} \right)} \,\Delta x\]Taking the limit will get the exact hydrostatic force,
\[F = \mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^n {19620x_i^*\left( {3 - \frac{3}{4}x_i^*} \right)} \,\Delta x\]Using the definition of the definite integral this is nothing more than,
\[F = \int_{{\,0}}^{{\,4}}{{19620\left( {3x - \frac{3}{4}{x^2}} \right)\,dx}}\]The hydrostatic force is then,
\[\begin{align*}F &= \int_{{\,0}}^{{\,4}}{{19620\left( {3x - \frac{3}{4}{x^2}} \right)\,dx}}\\ & = \left. {19620\left( {\frac{3}{2}{x^2} - \frac{1}{4}{x^3}} \right)} \right|_0^4\\ & = 156960\,N\end{align*}\]Let’s take a look at another example.
First, we’re going to assume that the top of the circular plate is 6 meters under the water. Next, we will set up the axis system so that the origin of the axis system is at the center of the plate. Setting the axis system up in this way will greatly simplify our work.
Finally, we will again split up the plate into \(n\) horizontal strips each of width \(\Delta y\) and we’ll choose a point \(y_i^*\) from each strip. We’ll also assume that the strips are rectangular again to help with the computations. Here is a sketch of the setup.
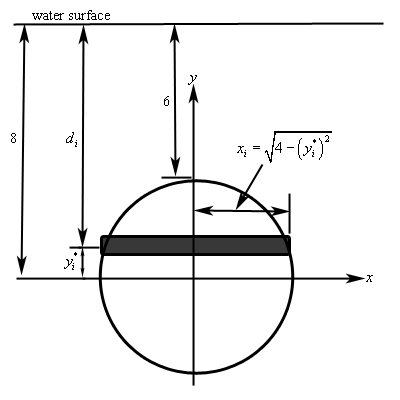
The depth below the water surface of each strip is,
\[{d_i} = 8 - y_i^*\]and that in turn gives us the pressure on the strip,
\[{P_i} = \rho g{d_i} = 9810\left( {8 - y_i^*} \right)\]The area of each strip is,
\[{A_i} = 2\sqrt {4 - {{\left( {y_i^*} \right)}^2}} \,\,\Delta y\]The hydrostatic force on each strip is,
\[{F_i} = {P_i}{A_i} = 9810\left( {8 - y_i^*} \right)\left( 2 \right)\sqrt {4 - {{\left( {y_i^*} \right)}^2}} \,\,\Delta y\]The total force on the plate is,
\[\begin{align*}F & = \mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^n {19620\left( {8 - y_i^*} \right)\sqrt {4 - {{\left( {y_i^*} \right)}^2}} \,\,\Delta y} \\ & = 19620\int_{{\, - 2}}^{{\,2}}{{\left( {8 - y} \right)\sqrt {4 - {y^2}} \,dy}}\end{align*}\]To do this integral we’ll need to split it up into two integrals.
\[F = 19620\int_{{\, - 2}}^{{\,2}}{{8\sqrt {4 - {y^2}} \,dy}} - 19620\int_{{\, - 2}}^{{\,2}}{{y\sqrt {4 - {y^2}} \,dy}}\]The first integral requires the trig substitution \(y = 2\sin \theta \) and the second integral needs the substitution \(v = 4 - {y^2}\). After using these substitutions we get,
\[\begin{align*}F & = 627840\int_{{\, - {\pi }/{2}\;}}^{{\,{\pi }/{2}\;}}{{{{\cos }^2}\theta \,d\theta }} + 9810\int_{{\,0}}^{{\,0}}{{\sqrt v \,dv}}\\ & = 313920\int_{{\, - {\pi }/{2}\;}}^{{\,{\pi }/{2}\;}}{{1 + \cos \left( {2\theta } \right)\,d\theta }} + 0\\ & = 313920\left. {\left( {\theta + \frac{1}{2}\sin \left( {2\theta } \right)} \right)} \right|_{ - \frac{\pi }{2}}^{\frac{\pi }{2}}\\ & = 313920\pi \end{align*}\]Note that after the substitution we know the second integral will be zero because the upper and lower limit is the same.