Appendix A.3 : Proof of Trig Limits
In this section we’re going to provide the proof of the two limits that are used in the derivation of the derivative of sine and cosine in the Derivatives of Trig Functions section of the Derivatives chapter.
Proof of : \(\displaystyle \mathop {\lim }\limits_{\theta \to 0} \frac{{\sin \theta }}{\theta } = 1\)
This proof of this limit uses the Squeeze Theorem. However, getting things set up to use the Squeeze Theorem can be a somewhat complex geometric argument that can be difficult to follow so we’ll try to take it fairly slow.
Let’s start by assuming that \(0 \le \theta \le \frac{\pi }{2}\). Since we are proving a limit that has \(\theta \to 0\) it’s okay to assume that \(\theta \) is not too large (i.e. \(\theta \le \frac{\pi }{2}\)). Also, by assuming that \(\theta \) is positive we’re actually going to first prove that the above limit is true if it is the right-hand limit. As you’ll see if we can prove this then the proof of the limit will be easy.
So, now that we’ve got our assumption on \(\theta \) taken care of let’s start off with the unit circle circumscribed by an octagon with a small slice marked out as shown below.
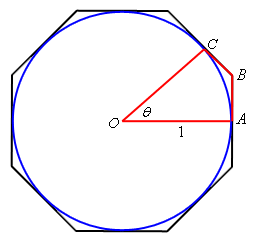
Points \(A\) and \(C\) are the midpoints of their respective sides on the octagon and are in fact tangent to the circle at that point. We’ll call the point where these two sides meet \(B\).
From this figure we can see that the circumference of the circle is less than the length of the octagon. This also means that if we look at the slice of the figure marked out above then the length of the portion of the circle included in the slice must be less than the length of the portion of the octagon included in the slice.
Because we’re going to be doing most of our work on just the slice of the figure let’s strip that out and look at just it. Here is a sketch of just the slice.
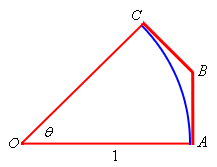
Now denote the portion of the circle by \({\mathop{\mbox{arc }}\nolimits} AC\) and the lengths of the two portion of the octagon shown by \(\left| {AB} \right|\) and \(\left| {BC} \right|\). Then by the observation about lengths we made above we must have,
\[\begin{equation}{\mathop{\mbox{arc }}\nolimits} AC < \left| {AB} \right| + \left| {BC} \right|\label{eq:eq1}\end{equation}\]Next, extend the lines \(AB\) and \(OC\) as shown below and call the point that they meet \(D\). The triangle now formed by \(AOD\) is a right triangle. All this is shown in the figure below.
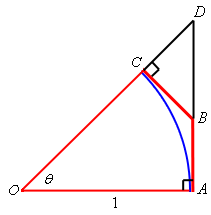
The triangle \(BCD\) is a right triangle with hypotenuse \(BD\) and so we know \(\left| {BC} \right| < \left| {BD} \right|\). Also notice that \(\left| {AB} \right| + \left| {BD} \right| = \left| {AD} \right|\). If we use these two facts in \(\eqref{eq:eq1}\) we get,
\[\begin{align}{\mathop{\mbox{arc }}\nolimits} AC & < \left| {AB} \right| + \left| {BC} \right| \nonumber \\ & < \left| {AB} \right| + \left| {BD} \right| \nonumber\\ & = \left| {AD} \right| \label{eq:eq2}\end{align}\]Next, as noted already the triangle \(AOD\) is a right triangle and so we can use a little right triangle trigonometry to write \(\left| {AD} \right| = \left| {AO} \right|\tan \theta \). Also note that \(\left| {AO} \right| = 1\) since it is nothing more than the radius of the unit circle. Using this information in \(\eqref{eq:eq2}\) gives,
\[\begin{align}{\mathop{\mbox{arc }}\nolimits} AC & < \left| {AD} \right| \nonumber\\ & < \left| {AO} \right|\tan \theta \nonumber\\ & = \tan \theta \label{eq:eq3} \end{align}\]The next thing that we need to recall is that the length of a portion of a circle is given by the radius of the circle times the angle (in radians!) that traces out the portion of the circle we’re trying to measure. For our portion this means that,
\[{\mathop{\mbox{arc }}\nolimits} AC = \left| {AO} \right|\theta = \theta \]Before proceeding a quick note. Students often ask why we always use radians in a Calculus class. This is the reason why! The formula for the length of a portion of a circle used above assumed that the angle is in radians. The formula for angles in degrees is different and if we used that we would get a different answer. So, remember to always use radians.
So, putting this into \(\eqref{eq:eq3}\) we see that,
\[\theta = {\mathop{\mbox{arc }}\nolimits} AC < \tan \theta = \frac{{\sin \theta }}{{\cos \theta }}\]or, if we do a little rearranging we get,
\[\begin{equation}\cos \theta < \frac{{\sin \theta }}{\theta }\label{eq:eq4}\end{equation}\]We’ll be coming back to \(\eqref{eq:eq4}\) in a bit. Let’s now add in a couple more lines into our figure above. Let’s connect \(A\) and \(C\) with a line and drop a line straight down from \(C\) until it intersects \(AO\) at a right angle and let’s call the intersection point \(E\). This is all shown in the figure below.
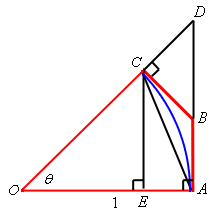
Okay, the first thing to notice here is that,
\[\begin{equation}\left| {CE} \right| < \left| {AC} \right| < {\mathop{\mbox{arc }}\nolimits} AC\label{eq:eq5}\end{equation}\]Also note that triangle \(EOC\) is a right triangle with a hypotenuse of \(\left| {CO} \right| = 1\). Using some right triangle trig we can see that,
\[\left| {CE} \right| = \left| {CO} \right|\sin \theta = \sin \theta \]Plugging this into \(\eqref{eq:eq5}\) and recalling that \({\mathop{\mbox{arc }}\nolimits} AC = \theta \) we get,
\[\sin \theta = \left| {CE} \right| < {\mathop{\mbox{arc }}\nolimits} AC = \theta \]and with a little rewriting we get,
\[\begin{equation}\frac{{\sin \theta }}{\theta } < 1 \label{eq:eq6} \end{equation}\]Okay, we’re almost done here. Putting \(\eqref{eq:eq4}\) and \(\eqref{eq:eq6}\) together we see that,
\[\cos \theta < \frac{{\sin \theta }}{\theta } < 1\]provided \(0 \le \theta \le \frac{\pi }{2}\). Let’s also note that,
\[\mathop {\lim }\limits_{\theta \to 0} \cos \theta = 1\hspace{0.75in}\mathop {\lim }\limits_{\theta \to 0} 1 = 1\]We are now set up to use the Squeeze Theorem. The only issue that we need to worry about is that we are staying to the right of \(\theta = 0\) in our assumptions and so the best that the Squeeze Theorem will tell us is,
\[\mathop {\lim }\limits_{\theta \to {0^ + }} \frac{{\sin \theta }}{\theta } = 1\]So, we know that the limit is true if we are only working with a right-hand limit. However we know that \(\sin \theta \) is an odd function and so,
\[\frac{{\sin \left( { - \theta } \right)}}{{ - \theta }} = \frac{{ - \sin \theta }}{{ - \theta }} = \frac{{\sin \theta }}{\theta }\]In other words, if we approach zero from the left (i.e. negative \(\theta \)’s) then we’ll get the same values in the function as if we’d approached zero from the right (i.e. positive \(\theta \)’s) and so,
\[\mathop {\lim }\limits_{\theta \to {0^ - }} \frac{{\sin \theta }}{\theta } = 1\]We have now shown that the two one-sided limits are the same and so we must also have,
\[\mathop {\lim }\limits_{\theta \to 0} \frac{{\sin \theta }}{\theta } = 1\]That was a somewhat long proof and if you’re not really good at geometric arguments it can be kind of daunting and confusing. Nicely, the second limit is very simple to prove, provided you’ve already proved the first limit.
Proof of : \(\displaystyle \mathop {\lim }\limits_{\theta \to 0} \frac{{\cos \theta - 1}}{\theta } = 0\)
We’ll start by doing the following,
\[\begin{equation}\mathop {\lim }\limits_{\theta \to 0} \frac{{\cos \theta - 1}}{\theta } = \mathop {\lim }\limits_{\theta \to 0} \frac{{\left( {\cos \theta - 1} \right)\left( {\cos \theta + 1} \right)}}{{\theta \left( {\cos \theta + 1} \right)}} = \mathop {\lim }\limits_{\theta \to 0} \frac{{{{\cos }^2}\theta - 1}}{{\theta \left( {\cos \theta + 1} \right)}} \label{eq:eq7} \end{equation}\]Now, let’s recall that,
\[{\cos ^2}\theta + {\sin ^2}\theta = 1\hspace{0.5in} \Rightarrow \hspace{0.5in}{\cos ^2}\theta - 1 = - {\sin ^2}\theta \]Using this in \(\eqref{eq:eq7}\) gives us,
\[\begin{align*}\mathop {\lim }\limits_{\theta \to 0} \frac{{\cos \theta - 1}}{\theta } & = \mathop {\lim }\limits_{\theta \to 0} \frac{{ - {{\sin }^2}\theta }}{{\theta \left( {\cos \theta + 1} \right)}}\\ & = \mathop {\lim }\limits_{\theta \to 0} \frac{{\sin \theta }}{\theta }\frac{{ - \sin \theta }}{{\cos \theta + 1}}\\ & = \mathop {\lim }\limits_{\theta \to 0} \frac{{\sin \theta }}{\theta }\,\,\,\mathop {\lim }\limits_{\theta \to 0} \frac{{ - \sin \theta }}{{\cos \theta + 1}}\end{align*}\]At this point, because we just proved the first limit and the second can be taken directly we’re pretty much done. All we need to do is take the limits.
\[\mathop {\lim }\limits_{\theta \to 0} \frac{{\cos \theta - 1}}{\theta } = \mathop {\lim }\limits_{\theta \to 0} \frac{{\sin \theta }}{\theta }\,\,\,\mathop {\lim }\limits_{\theta \to 0} \frac{{ - \sin \theta }}{{\cos \theta + 1}} = \left( 1 \right)\left( 0 \right) = 0\]