Section 12.4 : Quadric Surfaces
In the previous two sections we’ve looked at lines and planes in three dimensions (or \({\mathbb{R}^3}\)) and while these are used quite heavily at times in a Calculus class there are many other surfaces that are also used fairly regularly and so we need to take a look at those.
In this section we are going to be looking at quadric surfaces. Quadric surfaces are the graphs of any equation that can be put into the general form
\[A{x^2} + B{y^2} + C{z^2} + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0\]where \(A\), … , \(J\) are constants.
There is no way that we can possibly list all of them, but there are some standard equations so here is a list of some of the more common quadric surfaces.
Ellipsoid
Here is the general equation of an ellipsoid.
\[\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} = 1\]Here is a sketch of a typical ellipsoid.
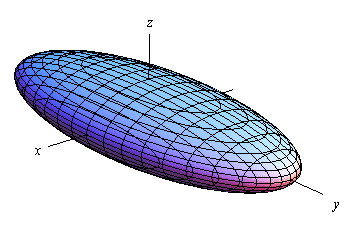
If \(a = b = c\) then we will have a sphere.
Notice that we only gave the equation for the ellipsoid that has been centered on the origin. Clearly ellipsoids don’t have to be centered on the origin. However, in order to make the discussion in this section a little easier we have chosen to concentrate on surfaces that are “centered” on the origin in one way or another.
Cone
Here is the general equation of a cone.
\[\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = \frac{{{z^2}}}{{{c^2}}}\]Here is a sketch of a typical cone.
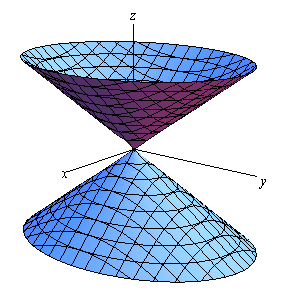
Now, note that while we called this a cone it is more of an hour glass shape rather than what most would call a cone. Of course, the upper and the lower portion of the hour glass really are cones as we would normally think of them.
That brings up the question of what if we really did just want the upper or lower portion (i.e. a cone in the traditional sense)? That is easy enough to answer. All we need to do is solve the given equation for \(z\) as follows,
\[{z^2} = {c^2}\left( {\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}}} \right) = \frac{{{c^2}}}{{{a^2}}}{x^2} + \frac{{{c^2}}}{{{b^2}}}{y^2} = {A^2}{x^2} + {B^2}{y^2}\,\,\,\,\, \to \,\,\,\,\,\,\,z = \pm \sqrt {{A^2}{x^2} + {B^2}{y^2}} \]We simplified the coefficients a little to make it the equation(s) easier to deal with. Now, we know that square roots always return positive numbers and so we can then see that \(z = \sqrt {{A^2}{x^2} + {B^2}{y^2}} \) will always be positive and so be the equation for just the upper portion of the “cone” above. Likewise, \(z = - \sqrt {{A^2}{x^2} + {B^2}{y^2}} \) will always be negative and so be the equation of just the lower portion of the “cone” above.
Also, note that this is the equation of a cone that will open along the \(z\)-axis. To get the equation of a cone that opens along one of the other axes all we need to do is make a slight modification of the equation. This will be the case for the rest of the surfaces that we’ll be looking at in this section as well.
In the case of a cone the variable that sits by itself on one side of the equal sign will determine the axis that the cone opens up along. For instance, a cone that opens up along the \(x\)-axis will have the equation,
\[\frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} = \frac{{{x^2}}}{{{a^2}}}\]For most of the following surfaces we will not give the other possible formulas. We will however acknowledge how each formula needs to be changed to get a change of orientation for the surface.
Cylinder
Here is the general equation of a cylinder.
\[\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\]This is a cylinder whose cross section is an ellipse. If \(a = b\) we have a cylinder whose cross section is a circle. We’ll be dealing with those kinds of cylinders more than the general form so the equation of a cylinder with a circular cross section is,
\[{x^2} + {y^2} = {r^2}\]Here is a sketch of typical cylinder with an ellipse cross section.
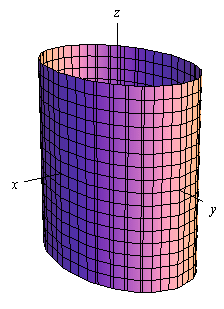
The cylinder will be centered on the axis corresponding to the variable that does not appear in the equation.
Be careful to not confuse this with a circle. In two dimensions it is a circle, but in three dimensions it is a cylinder.
Hyperboloid of One Sheet
Here is the equation of a hyperboloid of one sheet.
\[\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} - \frac{{{z^2}}}{{{c^2}}} = 1\]Here is a sketch of a typical hyperboloid of one sheet.
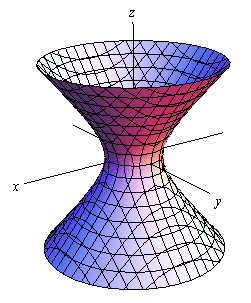
The variable with the negative in front of it will give the axis along which the graph is centered.
Hyperboloid of Two Sheets
Here is the equation of a hyperboloid of two sheets.
\[ - \frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} = 1\]Here is a sketch of a typical hyperboloid of two sheets.
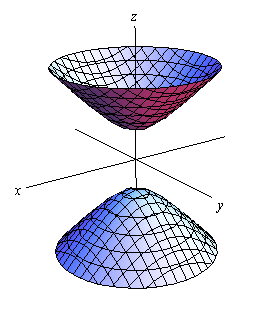
The variable with the positive in front of it will give the axis along which the graph is centered.
Notice that the only difference between the hyperboloid of one sheet and the hyperboloid of two sheets is the signs in front of the variables. They are exactly the opposite signs.
Also note that just as we could do with cones, if we solve the equation for \(z\) the positive portion will give the equation for the upper part of this while the negative portion will give the equation for the lower part of this.
Elliptic Paraboloid
Here is the equation of an elliptic paraboloid.
\[\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = \frac{z}{c}\]As with cylinders this has a cross section of an ellipse and if \(a = b\) it will have a cross section of a circle. When we deal with these we’ll generally be dealing with the kind that have a circle for a cross section.
Here is a sketch of a typical elliptic paraboloid.
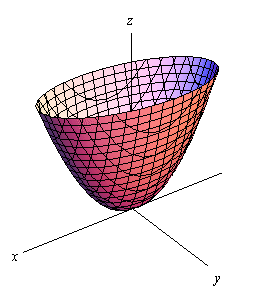
In this case the variable that isn’t squared determines the axis upon which the paraboloid opens up. Also, the sign of \(c\) will determine the direction that the paraboloid opens. If \(c\) is positive then it opens up and if \(c\) is negative then it opens down.
Hyperbolic Paraboloid
Here is the equation of a hyperbolic paraboloid.
\[\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = \frac{z}{c}\]Here is a sketch of a typical hyperbolic paraboloid.
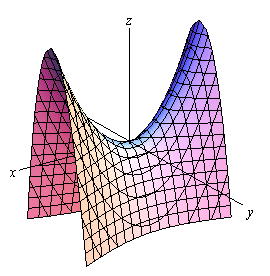
These graphs are vaguely saddle shaped and as with the elliptic paraboloid the sign of \(c\) will determine the direction in which the surface “opens up”. The graph above is shown for \(c\) positive.
With both of the types of paraboloids discussed above note that the surface can be easily moved up or down by adding/subtracting a constant from the left side.
For instance
\[z = - {x^2} - {y^2} + 6\]is an elliptic paraboloid that opens downward (be careful, the “-” is on the \(x\) and \(y\) instead of the \(z\)) and starts at \(z = 6\) instead of \(z = 0\).
Here are a couple of quick sketches of this surface.
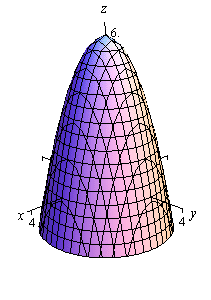
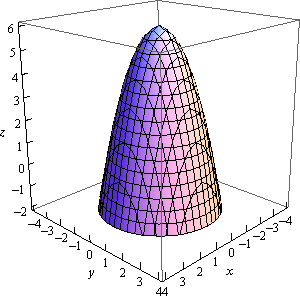
Note that we’ve given two forms of the sketch here. The sketch on the left has the standard set of axes but it is difficult to see the numbers on the axis. The sketch on the right has been “boxed” and this makes it easier to see the numbers to give a sense of perspective to the sketch. In most sketches that actually involve numbers on the axis system we will give both sketches to help get a feel for what the sketch looks like.