There are really just restatements of facts given in the basic exponential section of the review so we’ll leave it to you to go back and verify these.

\[\mathop {\lim }\limits_{x \to \infty } {{\bf{e}}^x} = \infty \hspace{0.5in}\mathop {\lim }\limits_{x \to - \infty } {{\bf{e}}^x} = 0\hspace{0.5in}\mathop {\lim }\limits_{x \to \infty } {{\bf{e}}^{ - x}} = 0\hspace{0.5in}\mathop {\lim }\limits_{x \to - \infty } {{\bf{e}}^{ - x}} = \infty \]

In this part what we need to note (using Fact 2 above) is that in the limit the exponent of the exponential does the following,

\[\mathop {\lim }\limits_{x \to \infty } \left( {2 - 4x - 8{x^2}} \right) = - \infty \]

So, the exponent goes to minus infinity in the limit and so the exponential must go to zero in the limit using the ideas from the previous set of examples. So, the answer here is,

\[\mathop {\lim }\limits_{x \to \infty } {{\bf{e}}^{2 - 4x - 8{x^2}}} = 0\]

Here let’s first note that,

\[\mathop {\lim }\limits_{t \to - \infty } \left( {{t^4} - 5{t^2} + 1} \right) = \infty \]

The exponent goes to infinity in the limit and so the exponential will also need to go to infinity in the limit. Or,

\[\mathop {\lim }\limits_{t \to - \infty } {{\bf{e}}^{{t^4} - 5{t^2} + 1}} = \infty \]

On the surface this part doesn’t appear to belong in this section since it isn’t a limit at infinity. However, it does fit into the ideas we’re examining in this set of examples.

So, let’s first note that using the idea from the previous section we have,

\[\mathop {\lim }\limits_{z \to {0^ + }} \frac{1}{z} = \infty \]

Remember that in order to do this limit here we do need to do a right-hand limit.

So, the exponent goes to infinity in the limit and so the exponential must also go to infinity.

Here’s the answer to this part.

\[\mathop {\lim }\limits_{z \to {0^ + }} {{\bf{e}}^{\frac{1}{z}}} = \infty \]

Let’s start by just taking the limit of each of the pieces and see what we get.

\[\mathop {\lim }\limits_{x \to \infty } \left( {{{\bf{e}}^{10x}} - 4{{\bf{e}}^{6x}} + 3{{\bf{e}}^x} + 2{{\bf{e}}^{ - 2x}} - 9{{\bf{e}}^{ - 15x}}} \right) = \infty - \infty + \infty + 0 - 0\]

The last two terms aren’t any problem (they will be in the next part however; do you see that?). The first three are a problem however as they present us with another indeterminate form.

When dealing with polynomials we factored out the term with the largest exponent in it. Let’s do the same thing here. However, we now have to deal with both positive and negative exponents and just what do we mean by the “largest” exponent. When dealing with these here we look at the terms that are causing the problems and ask “what is the largest exponent in those terms?”. So, since only the first three terms are causing us problems (i.e. they all evaluate to an infinity in the limit) we’ll look only at those.

So, since 10\(x\) is the largest of the three exponents there we’ll “factor” an \({{\bf{e}}^{10x}}\) out of the whole thing. Just as with polynomials we do the factoring by, in essence, dividing each term by \({{\bf{e}}^{10x}}\) and remembering that to simplify the division all we need to do is subtract the exponents. For example, let’s just take a look at the last term,

\[\frac{{ - 9{{\bf{e}}^{ - 15x}}}}{{{{\bf{e}}^{10x}}}} = - 9{{\bf{e}}^{ - 15x - 10x}} = - 9{{\bf{e}}^{ - 25x}}\]

Doing factoring on all terms then gives,

\[\mathop {\lim }\limits_{x \to \infty } \left( {{{\bf{e}}^{10x}} - 4{{\bf{e}}^{6x}} + 3{{\bf{e}}^x} + 2{{\bf{e}}^{ - 2x}} - 9{{\bf{e}}^{ - 15x}}} \right) = \mathop {\lim }\limits_{x \to \infty } \left[ {{{\bf{e}}^{10x}}\left( {1 - 4{{\bf{e}}^{ - 4x}} + 3{{\bf{e}}^{ - 9x}} + 2{{\bf{e}}^{ - 12x}} - 9{{\bf{e}}^{ - 25x}}} \right)} \right]\]

Notice that in doing this factoring all the remaining exponentials now have negative exponents and we know that for this limit (i.e. going out to positive infinity) these will all be zero in the limit and so will no longer cause problems.

We can now take the limit of the two factors. The first is clearly infinity and the second is clearly a finite number (one in this case) and so the Facts from the Infinite Limits section gives us the following limit,

\[\mathop {\lim }\limits_{x \to \infty } \left( {{{\bf{e}}^{10x}} - 4{{\bf{e}}^{6x}} + 3{{\bf{e}}^x} + 2{{\bf{e}}^{ - 2x}} - 9{{\bf{e}}^{ - 15x}}} \right) = \infty \]

To simplify the work here a little all we really needed to do was factor the \({{\bf{e}}^{10x}}\) out of the “problem” terms (the first three in this case) as follows,

\[\begin{align*}\mathop {\lim }\limits_{x \to \infty } \left( {{{\bf{e}}^{10x}} - 4{{\bf{e}}^{6x}} + 3{{\bf{e}}^x}} \right) & = \mathop {\lim }\limits_{x \to \infty } \left[ {{{\bf{e}}^{10x}}\left( {1 - 4{{\bf{e}}^{ - 4x}} + 3{{\bf{e}}^{ - 9x}}} \right) + 2{{\bf{e}}^{ - 2x}} - 9{{\bf{e}}^{ - 15x}}} \right]\\ & = \left( \infty \right)\left( 1 \right) + 0 - 0\\ & = \infty \end{align*}\]

We factored the \({{\bf{e}}^{10x}}\) out of all terms for the practice of doing the factoring and to avoid any issues with having the extra terms at the end. Note as well that while we wrote \(\left( \infty \right)\left( 1 \right)\) for the limit of the first term we are really using the Facts from the Infinite Limit section to do that limit.

Let’s start this one off in the same manner as the first part. Let’s take the limit of each of the pieces. This time note that because our limit is going to negative infinity the first three exponentials will in fact go to zero (because their exponents go to minus infinity in the limit). The final two exponentials will go to infinity in the limit (because their exponents go to plus infinity in the limit).

Taking the limits gives,

\[\mathop {\lim }\limits_{x \to - \infty } \left( {{{\bf{e}}^{10x}} - 4{{\bf{e}}^{6x}} + 3{{\bf{e}}^x} + 2{{\bf{e}}^{ - 2x}} - 9{{\bf{e}}^{ - 15x}}} \right) = 0 - 0 + 0 + \infty - \infty \]

So, the last two terms are the problem here as they once again leave us with an indeterminate form. As with the first example we’re going to factor out the “largest” exponent in the last two terms. This time however, “largest” doesn’t refer to the bigger of the two numbers (-2 is bigger than -15). Instead we’re going to use “largest” to refer to the exponent that is farther away from zero. Using this definition of “largest” means that we’re going to factor an \({{\bf{e}}^{ - 15x}}\) out.

Again, remember that to factor this out all we really are doing is dividing each term by \({{\bf{e}}^{ - 15x}}\) and then subtracting exponents. Here’s the work for the first term as an example,

\[\frac{{{{\bf{e}}^{10x}}}}{{{{\bf{e}}^{ - 15x}}}} = {{\bf{e}}^{10x - \left( { - 15x} \right)}} = {{\bf{e}}^{25x}}\]

As with the first part we can either factor it out of only the “problem” terms (i.e. the last two terms), or all the terms. For the practice we’ll factor it out of all the terms. Here is the factoring work for this limit,

\[\mathop {\lim }\limits_{x \to - \infty } \left( {{{\bf{e}}^{10x}} - 4{{\bf{e}}^{6x}} + 3{{\bf{e}}^x} + 2{{\bf{e}}^{ - 2x}} - 9{{\bf{e}}^{ - 15x}}} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {{{\bf{e}}^{ - 15x}}\left( {{{\bf{e}}^{25x}} - 4{{\bf{e}}^{21x}} + 3{{\bf{e}}^{16x}} + 2{{\bf{e}}^{13x}} - 9} \right)} \right]\]

Finally, after taking the limit of the two terms (the first is infinity and the second is a negative, finite number) and recalling the Facts from the Infinite Limit section we see that the limit is,

\[\mathop {\lim }\limits_{x \to - \infty } \left( {{{\bf{e}}^{10x}} - 4{{\bf{e}}^{6x}} + 3{{\bf{e}}^x} + 2{{\bf{e}}^{ - 2x}} - 9{{\bf{e}}^{ - 15x}}} \right) = - \infty \]

The basic concept involved in working this problem is the same as with rational expressions in the previous section. We look at the denominator and determine the exponential function with the “largest” exponent which we will then factor out from both numerator and denominator. We will use the same reasoning as we did with the previous example to determine the “largest” exponent. In the case since we are looking at a limit at plus infinity we only look at exponentials with positive exponents.

So, we’ll factor an \({{\bf{e}}^{4x}}\) out of both then numerator and denominator. Once that is done we can cancel the \({{\bf{e}}^{4x}}\) and then take the limit of the remaining terms. Here is the work for this limit,

\[\begin{align*}\mathop {\lim }\limits_{x \to \infty } \frac{{6{{\bf{e}}^{4x}} - {{\bf{e}}^{ - 2x}}}}{{8{{\bf{e}}^{4x}} - {{\bf{e}}^{2x}} + 3{{\bf{e}}^{ - x}}}} & = \mathop {\lim }\limits_{x \to \infty } \frac{{{{\bf{e}}^{4x}}\left( {6 - {{\bf{e}}^{ - 6x}}} \right)}}{{{{\bf{e}}^{4x}}\left( {8 - {{\bf{e}}^{ - 2x}} + 3{{\bf{e}}^{ - 5x}}} \right)}}\\ & = \mathop {\lim }\limits_{x \to \infty } \frac{{6 - {{\bf{e}}^{ - 6x}}}}{{8 - {{\bf{e}}^{ - 2x}} + 3{{\bf{e}}^{ - 5x}}}}\\ & = \frac{{6 - 0}}{{8 - 0 + 0}}\\ & = \frac{3}{4}\end{align*}\]

In this case we’re going to minus infinity in the limit and so we’ll look at exponentials in the denominator with negative exponents in determining the “largest” exponent. There’s only one however in this problem so that is what we’ll use.

Again, remember to only look at the denominator. Do NOT use the exponential from the numerator, even though that one is “larger” than the exponential in the denominator. We always look only at the denominator when determining what term to factor out regardless of what is going on in the numerator.

Here is the work for this part.

\[\begin{align*}\mathop {\lim }\limits_{x \to - \infty } \frac{{6{{\bf{e}}^{4x}} - {{\bf{e}}^{ - 2x}}}}{{8{{\bf{e}}^{4x}} - {{\bf{e}}^{2x}} + 3{{\bf{e}}^{ - x}}}} & = \mathop {\lim }\limits_{x \to - \infty } \frac{{{{\bf{e}}^{ - x}}\left( {6{{\bf{e}}^{5x}} - {{\bf{e}}^{ - x}}} \right)}}{{{{\bf{e}}^{ - x}}\left( {8{{\bf{e}}^{5x}} - {{\bf{e}}^{3x}} + 3} \right)}}\\ & = \mathop {\lim }\limits_{x \to - \infty } \frac{{6{{\bf{e}}^{5x}} - {{\bf{e}}^{ - x}}}}{{8{{\bf{e}}^{5x}} - {{\bf{e}}^{3x}} + 3}}\\ & = \frac{{0 - \infty }}{{0 - 0 + 3}}\\ & = - \infty \end{align*}\]

We’ll do the work on this part with much less detail.

\[\begin{align*}\mathop {\lim }\limits_{t \to - \infty } \frac{{{{\bf{e}}^{6t}} - 4{{\bf{e}}^{ - 6t}}}}{{2{{\bf{e}}^{3t}} - 5{{\bf{e}}^{ - 9t}} + {{\bf{e}}^{ - 3t}}}} & = \mathop {\lim }\limits_{t \to - \infty } \frac{{{{\bf{e}}^{ - 9t}}\left( {{{\bf{e}}^{15t}} - 4{{\bf{e}}^{3t}}} \right)}}{{{{\bf{e}}^{ - 9t}}\left( {2{{\bf{e}}^{12t}} - 5 + {{\bf{e}}^{6t}}} \right)}}\\ & = \mathop {\lim }\limits_{t \to - \infty } \frac{{{{\bf{e}}^{15t}} - 4{{\bf{e}}^{3t}}}}{{2{{\bf{e}}^{12t}} - 5 + {{\bf{e}}^{6t}}}}\\ & = \frac{{0 - 0}}{{0 - 5 + 0}}\\ & = 0\end{align*}\]

As with the last example I’ll leave it to you to verify these restatements from the basic logarithm section.

\[\mathop {\lim }\limits_{x \to {0^ + }} \ln x = - \infty \hspace{0.5in}\hspace{0.25in}\mathop {\lim }\limits_{x \to \infty } \ln x = \infty \]

Note that we had to do a right-handed limit for the first one since we can’t plug negative \(x\)’s into a logarithm. This means that the normal limit won’t exist since we must look at \(x\)’s from both sides of the point in question and \(x\)’s to the left of zero are negative.

So, let’s first look to see what the argument of the log is doing,

\[\mathop {\lim }\limits_{x \to \infty } \left( {7{x^3} - {x^2} + 1} \right) = \infty \]

The argument of the log is going to infinity and so the log must also be going to infinity in the limit. The answer to this part is then,

\[\mathop {\lim }\limits_{x \to \infty } \ln \left( {7{x^3} - {x^2} + 1} \right) = \infty \]

First, note that the limit going to negative infinity here isn’t a violation (necessarily) of the fact that we can’t plug negative numbers into the logarithm. The real issue is whether or not the argument of the log will be negative or not.

Using the techniques from earlier in this section we can see that,

\[\mathop {\lim }\limits_{t \to - \infty } \frac{1}{{{t^2} - 5t}} = 0\]

and let’s also note that for negative numbers (which we can assume we’ve got since we’re going to minus infinity in the limit) the denominator will always be positive and so the quotient will also always be positive. Therefore, not only does the argument go to zero, it goes to zero from the right. This is exactly what we need to do this limit.

So, the answer here is,

\[\mathop {\lim }\limits_{t \to - \infty } \ln \left( {\frac{1}{{{t^2} - 5t}}} \right) = - \infty \]

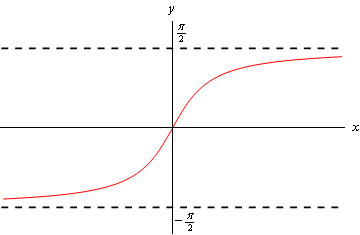
As noted above all we really need to do here is look at the graph of the inverse tangent. Doing this shows us that we have the following value of the limit.

\[\mathop {\lim }\limits_{x \to \infty } {\tan ^{ - 1}}x = \frac{\pi }{2}\]

Again, not much to do here other than examine the graph of the inverse tangent.

\[\mathop {\lim }\limits_{x \to - \infty } {\tan ^{ - 1}}x = - \frac{\pi }{2}\]

Okay, in part (a) above we saw that if the argument of the inverse tangent function (the stuff inside the parenthesis) goes to plus infinity then we know the value of the limit. In this case (using the techniques from the previous section) we have,

\[\mathop {\lim }\limits_{x \to \infty } {x^3} - 5x + 6 = \infty \]

So, this limit is,

\[\mathop {\lim }\limits_{x \to \infty } {\tan ^{ - 1}}\left( {{x^3} - 5x + 6} \right) = \frac{\pi }{2}\]

Even though this limit is not a limit at infinity we’re still looking at the same basic idea here. We’ll use part (b) from above as a guide for this limit. We know from the Infinite Limits section that we have the following limit for the argument of this inverse tangent,

\[\mathop {\lim }\limits_{x \to {0^ - }} \frac{1}{x} = - \infty \]

So, since the argument goes to minus infinity in the limit we know that this limit must be,

\[\mathop {\lim }\limits_{x \to {0^ - }} {\tan ^{ - 1}}\left( {\frac{1}{x}} \right) = - \frac{\pi }{2}\]