Section 2.8 : Applications of Quadratic Equations
In this section we’re going to go back and revisit some of the applications that we saw in the Linear Applications section and see some examples that will require us to solve a quadratic equation to get the answer.
Note that the solutions in these cases will almost always require the quadratic formula so expect to use it and don’t get excited about it. Also, we are going to assume that you can do the quadratic formula work and so we won’t be showing that work. We will give the results of the quadratic formula, we just won’t be showing the work.
Also, as we will see, we will need to get decimal answer to these and so as a general rule here we will round all answers to 4 decimal places.
So, we’ll let \(x\) be the length of the field and so we know that \(x + 3\) will be the width of the field. Now, we also know that area of a rectangle is length times width and so we know that,
\[x\left( {x + 3} \right) = 75\]Now, this is a quadratic equation so let’s first write it in standard form.
\[\begin{align*}{x^2} + 3x & = 75\\ {x^2} + 3x - 75 & = 0\end{align*}\]Using the quadratic formula gives,
\[x = \frac{{ - 3 \pm \sqrt {309} }}{2}\]Now, at this point, we’ve got to deal with the fact that there are two solutions here and we only want a single answer. So, let’s convert to decimals and see what the solutions actually are.
\[x = \frac{{ - 3 + \sqrt {309} }}{2} = 7.2892\hspace{0.25in}{\mbox{and}}\hspace{0.25in}x = \frac{{ - 3 - \sqrt {309} }}{2} = - 10.2892\]So, we have one positive and one negative. From the stand point of needing the dimensions of a field the negative solution doesn’t make any sense so we will ignore it.
Therefore, the length of the field is 7.2892 feet. The width is 3 feet longer than this and so is 10.2892 feet.
Notice that the width is almost the second solution to the quadratic equation. The only difference is the minus sign. Do NOT expect this to always happen. In this case this is more of a function of the problem. For a more complicated set up this will NOT happen.
Now, from a physical standpoint we can see that we should expect to NOT get complex solutions to these problems. Upon solving the quadratic equation we should get either two real distinct solutions or a double root. Also, as the previous example has shown, when we get two real distinct solutions we will be able to eliminate one of them for physical reasons.
Let’s work another example or two.
We’ll start off by letting \(t\) be the amount of time that the first car, let’s call it car A, travels. Since the second car, let’s call that car B, starts out two hours later then we know that it will travel for \(t - 2\) hours.
Now, we know that the distance traveled by an object (or car since that’s what we’re dealing with here) is its speed times time traveled. So we have the following distances traveled for each car.
\[\begin{array}{l}{\mbox{distance of car A : }}25t\\ {\mbox{distance of car B : }}20\left( {t - 2} \right)\end{array}\]At this point a quick sketch of the situation is probably in order so we can see just what is going on. In the sketch we will assume that the two cars have traveled long enough so that they are 300 miles apart.
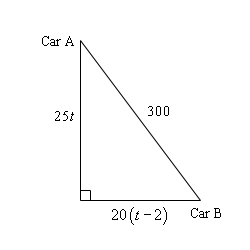
So, we have a right triangle here. That means that we can use the Pythagorean Theorem to say,
\[{\left( {25t} \right)^2} + {\left( {20\left( {t - 2} \right)} \right)^2} = {\left( {300} \right)^2}\]This is a quadratic equation, but it is going to need some fairly heavy simplification before we can solve it so let’s do that.
\[\begin{align*}625{t^2} + {\left( {20t - 40} \right)^2} & = 90000\\ 625{t^2} + 400{t^2} - 1600t + 1600 & = 90000\\ 1025{t^2} - 1600t - 88400 & = 0\end{align*}\]Now, the coefficients here are quite large, but that is just something that will happen fairly often with these problems so don’t worry about that. Using the quadratic formula (and simplifying that answer) gives,
\[t = \frac{{1600 \pm \sqrt {365000000} }}{{2050}} = \frac{{1600 \pm 1000\sqrt {365} }}{{2050}} = \frac{{32 \pm 20\sqrt {365} }}{{41}}\]Again, we have two solutions and we’re going to need to determine which one is the correct one, so let’s convert them to decimals.
\[t = \frac{{32 + 20\sqrt {365} }}{{41}} = 10.09998\hspace{0.25in}\hspace{0.25in}{\mbox{and }}\hspace{0.25in}\,\,\,\,\,\,\,\,\,\,\,t = \frac{{32 - 20\sqrt {365} }}{{41}} = - 8.539011\]As with the previous example the negative answer just doesn’t make any sense. So, it looks like the car A traveled for 10.09998 hours when they were finally 300 miles apart.
Also, even though the problem didn’t ask for it, the second car will have traveled for 8.09998 hours before they are 300 miles apart. Notice as well that this is NOT the second solution without the negative this time, unlike the first example.
Let \(t\) be the amount of time it takes the first machine (Machine A) to stuff a batch of envelopes by itself. That means that it will take the second machine (Machine B) \(t + 1\) hours to stuff a batch of envelopes by itself.
The word equation for this problem is then,
\[\begin{align*}\left( \begin{array}{c}{\mbox{Portion of job }}\\ {\mbox{done by Machine A}}\end{array} \right) + \left( \begin{array}{c}{\mbox{Portion of job }}\\ {\mbox{done by Machine B}}\end{array} \right) & = 1{\mbox{ Job}}\\ \\ \left( \begin{array}{c}{\mbox{Work Rate}}\\ {\mbox{of Machine A}}\end{array} \right)\left( \begin{array}{c}{\mbox{Time Spent}}\\ {\mbox{Working}}\end{array} \right) + \left( \begin{array}{c}{\mbox{Work Rate}}\\ {\mbox{of Machine B}}\end{array} \right)\left( \begin{array}{c}{\mbox{Time Spent}}\\ {\mbox{Working}}\end{array} \right) & = 1\end{align*}\]We know the time spent working together (2 hours) so we need to work rates of each machine. Here are those computations.
\[1{\mbox{ Job}} = \left( {{\mbox{Work Rate of Machine A}}} \right) \times \left( t \right)\hspace{0.25in} \Rightarrow \hspace{0.25in}{\mbox{Machine A}} = \frac{1}{t}\] \[1{\mbox{ Job}} = \left( {{\mbox{Work Rate of Machine B}}} \right) \times \left( {t + 1} \right)\hspace{0.25in} \Rightarrow \hspace{0.25in}{\mbox{Machine B}} = \frac{1}{{t + 1}}\]Note that it’s okay that the work rates contain \(t\). In fact, they will need to so we can solve for it! Plugging into the word equation gives,
\[\begin{align*}\left( {\frac{1}{t}} \right)\left( 2 \right) + \left( {\frac{1}{{t + 1}}} \right)\left( 2 \right) & = 1\\ \frac{2}{t} + \frac{2}{{t + 1}} & = 1\end{align*}\]So, to solve we’ll first need to clear denominators and get the equation in standard form.
\[\begin{align*}\left( {\frac{2}{t} + \frac{2}{{t + 1}}} \right)\left( t \right)\left( {t + 1} \right) & = \left( 1 \right)\left( t \right)\left( {t + 1} \right)\\ 2\left( {t + 1} \right) + 2t & = {t^2} + t\\ 4t + 2 &= {t^2} + t\\ 0 & = {t^2} - 3t - 2\end{align*}\]Using the quadratic formula gives,
\[t = \frac{{3 \pm \sqrt {17} }}{2}\]Converting to decimals gives,
\[t = \frac{{3 + \sqrt {17} }}{2} = 3.5616\hspace{0.25in}\hspace{0.25in}{\mbox{and}}\hspace{0.25in}\hspace{0.25in}t = \frac{{3 - \sqrt {17} }}{2} = - 0.5616\]Again, the negative doesn’t make any sense and so Machine A will work for 3.5616 hours to stuff a batch of envelopes by itself. Machine B will need 4.5616 hours to stuff a batch of envelopes by itself. Again, unlike the first example, note that the time for Machine B was NOT the second solution from the quadratic without the minus sign.