Section 7.3 : Trig Substitutions
As we have done in the last couple of sections, let’s start off with a couple of integrals that we should already be able to do with a standard substitution.
\[\int{{x\sqrt {25{x^2} - 4} \,dx}} = \frac{1}{{75}}{\left( {25{x^2} - 4} \right)^{\frac{3}{2}}} + c\hspace{0.5in}\int{{\frac{x}{{\sqrt {25{x^2} - 4} }}\,dx}} = \frac{1}{{25}}\sqrt {25{x^2} - 4} + c\]Both of these used the substitution \(u = 25{x^2} - 4\) and at this point should be pretty easy for you to do. However, let’s take a look at the following integral.
In this case the substitution \(u = 25{x^2} - 4\) will not work (we don’t have the \(x\,dx\) in the numerator the substitution needs) and so we’re going to have to do something different for this integral.
It would be nice if we could reduce the two terms in the root down to a single term somehow. The following substitution will do that for us.
\[x = \frac{2}{5}\sec \theta \]Do not worry about where this came from at this point. As we work the problem you will see that it works and that if we have a similar type of square root in the problem we can always use a similar substitution.
Before we actually do the substitution however let’s verify the claim that this will allow us to reduce the two terms in the root to a single term.
\[\sqrt {25{x^2} - 4} = \sqrt {25\left( {\frac{4}{{25}}} \right){{\sec }^2}\theta - 4} = \sqrt {4\left( {{{\sec }^2}\theta - 1} \right)} = 2\sqrt {{{\sec }^2}\theta - 1} \]Now reduce the two terms to a single term all we need to do is recall the relationship,
\[{\tan ^2}\theta + 1 = {\sec ^2}\theta \hspace{0.25in}\,\,\,\,\, \Rightarrow \hspace{0.5in}{\sec ^2}\theta - 1 = {\tan ^2}\theta \]Using this fact the square root becomes,
\[\sqrt {25{x^2} - 4} = 2\sqrt {{{\tan }^2}\theta } = 2\left| {\tan \theta } \right|\]So, not only were we able to reduce the two terms to a single term in the process we were able to easily eliminate the root as well!
Note, however, the presence of the absolute value bars. These are important. Recall that
\[\sqrt {{x^2}} = \left| x \right|\]There should always be absolute value bars at this stage. If we knew that \(\tan \theta \) was always positive or always negative we could eliminate the absolute value bars using,
\[\left| x \right| = \left\{ {\begin{array}{rl}x&{{\mbox{if }}x \ge 0}\\{ - x}&{{\mbox{if }}x < 0}\end{array}} \right.\]Without limits we won’t be able to determine if \(\tan \theta \) is positive or negative, however, we will need to eliminate them in order to do the integral. Therefore, since we are doing an indefinite integral we will assume that \(\tan \theta \) will be positive and so we can drop the absolute value bars. This gives,
\[\sqrt {25{x^2} - 4} = 2\tan \theta \]So, we were able to reduce the two terms under the root to a single term with this substitution and in the process eliminate the root as well. Eliminating the root is a nice side effect of this substitution as the problem will now become somewhat easier to do.
Let’s now do the substitution and see what we get. In doing the substitution don’t forget that we’ll also need to substitute for the \(dx\). This is easy enough to get from the substitution.
\[x = \frac{2}{5}\sec \theta \hspace{0.5in} \Rightarrow \hspace{0.25in}\,\,\,\,\,dx = \frac{2}{5}\sec \theta \tan \theta \,d\theta \]Using this substitution the integral becomes,
\[\begin{align*}\int{{\frac{{\sqrt {25{x^2} - 4} }}{x}\,dx}} & = \int{{\frac{{2\tan \theta }}{{\frac{2}{5}\sec \theta }}\,\left( {\frac{2}{5}\sec \theta \tan \theta } \right)d\theta }}\\ & = 2\int{{{{\tan }^2}\theta \,d\theta }}\end{align*}\]With this substitution we were able to reduce the given integral to an integral involving trig functions and we saw how to do these problems in the previous section. Let’s finish the integral.
\[\begin{align*}\int{{\frac{{\sqrt {25{x^2} - 4} }}{x}\,dx}} & = 2\int{{{{\sec }^2}\theta - 1\,d\theta }}\\ & = 2\left( {\tan \theta - \theta } \right) + c\end{align*}\]So, we’ve got an answer for the integral. Unfortunately, the answer isn’t given in \(x\)’s as it should be. So, we need to write our answer in terms of \(x\). We can do this with some right triangle trig. From our original substitution we have,
\[\sec \theta = \frac{{5x}}{2} = \frac{{{\mbox{hypotenuse}}}}{{{\mbox{adjacent}}}}\]This gives the following right triangle.
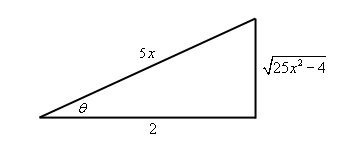
From this we can see that,
\[\tan \theta = \frac{{\sqrt {25{x^2} - 4} }}{2}\]We can deal with the \(\theta \) in one of any variety of ways. From our substitution we can see that,
\[\theta = {\sec ^{ - 1}}\left( {\frac{{5x}}{2}} \right)\]While this is a perfectly acceptable method of dealing with the \(\theta \) we can use any of the possible six inverse trig functions and since sine and cosine are the two trig functions most people are familiar with we will usually use the inverse sine or inverse cosine. In this case we’ll use the inverse cosine.
\[\theta = {\cos ^{ - 1}}\left( {\frac{2}{{5x}}} \right)\]So, with all of this the integral becomes,
\[\begin{align*}\int{{\frac{{\sqrt {25{x^2} - 4} }}{x}\,dx}} & = 2\left( {\frac{{\sqrt {25{x^2} - 4} }}{2} - {{\cos }^{ - 1}}\left( {\frac{2}{{5x}}} \right)} \right) + c\\ & = \sqrt {25{x^2} - 4} - 2{\cos ^{ - 1}}\left( {\frac{2}{{5x}}} \right) + c\end{align*}\]We now have the answer back in terms of \(x\).
Wow! That was a lot of work. Most of these won’t take as long to work however. This first one needed lots of explanation since it was the first one. The remaining examples won’t need quite as much explanation and so won’t take as long to work.
However, before we move onto more problems let’s first address the issue of definite integrals and how the process differs in these cases.
The limits here won’t change the substitution so that will remain the same.
\[x = \frac{2}{5}\sec \theta \]Using this substitution the square root still reduces down to,
\[\sqrt {25{x^2} - 4} = 2\left| {\tan \theta } \right|\]However, unlike the previous example we can’t just drop the absolute value bars. In this case we’ve got limits on the integral and so we can use the limits as well as the substitution to determine the range of \(\theta \) that we’re in. Once we’ve got that we can determine how to drop the absolute value bars.
Here’s the limits of \(\theta \) and note that if you aren’t good at solving trig equations in terms of secant you can always convert to cosine as we do below.
\[\begin{align*}x & = \frac{2}{5}\,\,\,:\,\,\,\frac{2}{5} = \frac{2}{5}\sec \theta = \frac{2}{5}\frac{1}{{\cos \theta }}\hspace{0.25in} \to \hspace{0.25in}\cos \theta = 1\hspace{0.25in}\,\, \Rightarrow \hspace{0.25in}\,\,\theta = {\cos ^{ - 1}}\left( 1 \right) = 0\\ x & = \frac{4}{5}\,\,\,:\,\,\,\frac{4}{5} = \frac{2}{5}\sec \theta = \frac{2}{5}\frac{1}{{\cos \theta }}\hspace{0.25in} \to \hspace{0.25in}\cos \theta = \frac{1}{2}\hspace{0.25in} \Rightarrow \hspace{0.25in}\,\,\theta = {\cos ^{ - 1}}\left( {\frac{1}{2}} \right) = \frac{\pi }{3}\end{align*}\]Now, we know from solving trig equations, that there are in fact an infinite number of possible answers we could use. In fact, the more “correct” answer for the above work is,
\[\theta = 0 + 2\pi n = 2\pi n\hspace{0.25in}\& \hspace{0.25in} \theta = \frac{\pi }{3} + 2\pi n\hspace{0.25in} n = 0, \pm 1, \pm 2, \pm 3, \ldots \]So, which ones should we use? The answer is simple. When using a secant trig substitution and converting the limits we always assume that \(\theta \) is in the range of inverse secant. Or,
\[{\mbox{If }}\theta = {\sec ^{ - 1}}\left( x \right)\,\,{\mbox{then}}\,\,0 \le \theta < \frac{\pi }{2}\,\,{\mbox{or}}\,\,\frac{\pi }{2} < \theta \le \pi \]Note that we have to avoid \(\theta = \frac{\pi }{2}\) because secant will not exist at that point. Also note that the range of \(\theta \) was given in terms of secant even though we actually used inverse cosine to get the answers. This will not be a problem because even though inverse cosine can give \(\theta = \frac{\pi }{2}\) we’ll never get it in our work above because that would require that we started with the secant being undefined and that will not happen when converting the limits as that would in turn require one of the limits to also be undefined!
So, in finding the new limits we didn’t need all possible values of \(\theta \) we just need the inverse cosine answers we got when we converted the limits. Therefore, if we are in the range \(\frac{2}{5} \le x \le \frac{4}{5}\) then \(\theta \) is in the range of \(0 \le \theta \le \frac{\pi }{3}\) and in this range of \(\theta \)’s tangent is positive and so we can just drop the absolute value bars.
Let’s do the substitution. Note that the work is identical to the previous example and so most of it is left out. We’ll pick up at the final integral and then do the substitution.
\[\begin{align*}\int_{{\,\frac{2}{5}}}^{{\,\frac{4}{5}}}{{\frac{{\sqrt {25{x^2} - 4} }}{x}\,dx}} & = 2\int_{{\,0}}^{{\,\frac{\pi }{3}}}{{{{\sec }^2}\theta - 1\,d\theta }}\\ & = 2\left. {\left( {\tan \theta - \theta } \right)} \right|_0^{{\pi }/{3}\;}\\ & = 2\sqrt 3 - \frac{{2\pi }}{3}\end{align*}\]Note that because of the limits we didn’t need to resort to a right triangle to complete the problem.
Let’s take a look at a different set of limits for this integral.
Again, the substitution and square root are the same as the first two examples.
\[x = \frac{2}{5}\sec \theta \hspace{0.5in}\sqrt {25{x^2} - 4} = 2\left| {\tan \theta } \right|\]Let’s next see the limits \(\theta \) for this problem.
\[\begin{align*}x & = - \frac{2}{5}\,\,\,:\,\,\, - \frac{2}{5} = \frac{2}{5}\sec \theta = \frac{2}{5}\frac{1}{{\cos \theta }}\hspace{0.25in} \to \hspace{0.25in}\cos \theta = - 1\hspace{0.25in}\,\, \Rightarrow \hspace{0.25in}\,\,\theta = {\cos ^{ - 1}}\left( { - 1} \right) = \pi \\ x & = - \frac{4}{5}\,\,\,:\,\,\, - \frac{4}{5} = \frac{2}{5}\sec \theta = \frac{2}{5}\frac{1}{{\cos \theta }}\hspace{0.25in} \to \hspace{0.25in}\cos \theta = - \frac{1}{2}\hspace{0.25in} \Rightarrow \hspace{0.25in}\,\,\theta = {\cos ^{ - 1}}\left( { - \frac{1}{2}} \right) = \frac{{2\pi }}{3}\end{align*}\]Remember that in converting the limits we use the results from the inverse secant/cosine. So, for this range of \(x\)’s we have \(\frac{{2\pi }}{3} \le \theta \le \pi \) and in this range of \(\theta \) tangent is negative and so in this case we can drop the absolute value bars, but will need to add in a minus sign upon doing so. In other words,
\[\sqrt {25{x^2} - 4} = - 2\tan \theta \]So, the only change this will make in the integration process is to put a minus sign in front of the integral. The integral is then,
\[\begin{align*}\int_{{\, - \,\frac{4}{5}}}^{{\, - \,\frac{2}{5}}}{{\frac{{\sqrt {25{x^2} - 4} }}{x}\,dx}} & = - 2\int_{{\,\frac{{2\pi }}{3}}}^{{\,\pi }}{{{{\sec }^2}\theta - 1\,d\theta }}\\ & = - 2\left. {\left( {\tan \theta - \theta } \right)} \right|_{{{2\pi }}/{3}\;}^\pi \\ & = \frac{{2\pi }}{3} - 2\sqrt 3 \end{align*}\]In the last two examples we saw that we have to be very careful with definite integrals. We need to make sure that we determine the limits on \(\theta \) and whether or not this will mean that we can just drop the absolute value bars or if we need to add in a minus sign when we drop them.
Before moving on to the next example let’s get the general form for the secant trig substitution that we used in the previous set of examples and the assumed limits on \(\theta \).
Let’s work a new and different type of example.
Now, the terms under the root in this problem looks to be (almost) the same as the previous ones so let’s try the same type of substitution and see if it will work here as well.
\[x = 3\sec \theta \]Using this substitution, the square root becomes,
\[\sqrt {9 - {x^2}} = \sqrt {9 - 9{{\sec }^2}\theta } = 3\sqrt {1 - {{\sec }^2}\theta } = 3\sqrt { - {{\tan }^2}\theta } \]So, using this substitution we will end up with a negative quantity (the tangent squared is always positive of course) under the square root and this will be trouble. Using this substitution will give complex values and we don’t want that. So, using secant for the substitution won’t work.
However, the following substitution (and differential) will work.
\[x = 3\sin \theta \hspace{0.5in}\hspace{0.25in}dx = 3\cos \theta \,d\theta \]With this substitution the square root is,
\[\sqrt {9 - {x^2}} = 3\sqrt {1 - {{\sin }^2}\theta } = 3\sqrt {{{\cos }^2}\theta } = 3\left| {\cos \theta } \right| = 3\cos \theta \]We were able to drop the absolute value bars because we are doing an indefinite integral and so we’ll assume that everything is positive.
The integral is now,
\[\begin{align*}\int{{\frac{1}{{{x^4}\sqrt {9 - {x^2}} }}\,dx}} & = \int{{\frac{1}{{81{{\sin }^4}\theta \left( {3\cos \theta } \right)}}\,3\cos \theta \,d\theta }}\\ & = \frac{1}{{81}}\int{{\frac{1}{{{{\sin }^4}\theta }}\,d\theta }}\\ & = \frac{1}{{81}}\int{{{{\csc }^4}\theta \,d\theta }}\end{align*}\]In the previous section we saw how to deal with integrals in which the exponent on the secant was even and since cosecants behave an awful lot like secants we should be able to do something similar with this.
Here is the integral.
\[\begin{align*}\int{{\frac{1}{{{x^4}\sqrt {9 - {x^2}} }}\,dx}} & = \frac{1}{{81}}\int{{{{\csc }^2}\theta \,{{\csc }^2}\theta \,d\theta }}\\ & = \frac{1}{{81}}\int{{\left( {{{\cot }^2}\theta + 1} \right)\,{{\csc }^2}\theta \,d\theta }}\hspace{0.5in}u = \cot \theta \\ & = - \frac{1}{{81}}\int{{{u^2} + 1\,du}}\\ & = - \frac{1}{{81}}\left( {\frac{1}{3}{{\cot }^3}\theta + \cot \theta } \right) + c\end{align*}\]Now we need to go back to \(x\)’s using a right triangle. Here is the right triangle for this problem and trig functions for this problem.
\[\sin \theta = \frac{x}{3}\hspace{0.5in}\cot \theta = \frac{{\sqrt {9 - {x^2}} }}{x}\]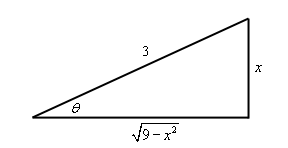
The integral is then,
\[\begin{align*}\int{{\frac{1}{{{x^4}\sqrt {9 - {x^2}} }}\,dx}} & = - \frac{1}{{81}}\left( {\frac{1}{3}{{\left( {\frac{{\sqrt {9 - {x^2}} }}{x}} \right)}^3} + \frac{{\sqrt {9 - {x^2}} }}{x}} \right) + c\\ & = - \frac{{{{\left( {9 - {x^2}} \right)}^{\frac{3}{2}}}}}{{243{x^3}}} - \frac{{\sqrt {9 - {x^2}} }}{{81x}} + c\end{align*}\]We aren’t going to be doing a definite integral example with a sine trig substitution. However, if we had we would need to convert the limits and that would mean eventually needing to evaluate an inverse sine. So, much like with the secant trig substitution, the values of \(\theta \) that we’ll use will be those from the inverse sine or,
\[{\mbox{If }}\theta = {\sin ^{ - 1}}\left( x \right)\,\,{\mbox{then}}\,\, - \frac{\pi }{2} \le \theta \le \frac{\pi }{2}\]Here is a summary for the sine trig substitution.
There is one final case that we need to look at. The next integral will also contain something that we need to make sure we can deal with.
First, notice that there really is a square root in this problem even though it isn’t explicitly written out. To see the root let’s rewrite things a little.
\[{\left( {36{x^2} + 1} \right)^{\frac{3}{2}}} = {\left( {{{\left( {36{x^2} + 1} \right)}^{\frac{1}{2}}}} \right)^3} = {\left( {\sqrt {36{x^2} + 1} } \right)^3}\]This terms under the root are not in the form we saw in the previous examples. Here we will use the substitution for this root.
\[x = \frac{1}{6}\tan \theta \hspace{0.5in}\hspace{0.25in}dx = \frac{1}{6}{\sec ^2}\theta \,d\theta \]With this substitution the denominator becomes,
\[{\left( {\sqrt {36{x^2} + 1} } \right)^3} = {\left( {\sqrt {{{\tan }^2}\theta + 1} } \right)^3} = {\left( {\sqrt {{{\sec }^2}\theta } } \right)^3} = {\left| {\sec \theta } \right|^3}\]Now, because we have limits we’ll need to convert them to \(\theta \) so we can determine how to drop the absolute value bars.
\[\begin{align*}x & = 0\,\,\,:\,\,\,0 = \frac{1}{6}\tan \theta \hspace{0.25in}\,\,\, \Rightarrow \hspace{0.25in}\,\,\theta = {\tan ^{ - 1}}\left( 0 \right) = 0\\ x &= \frac{1}{6}\,\,\,:\,\,\,\frac{1}{6} = \frac{1}{6}\tan \theta \hspace{0.25in}\, \Rightarrow \hspace{0.25in}\,\,\theta = {\tan ^{ - 1}}\left( 1 \right) = \frac{\pi }{4}\end{align*}\]As with the previous two cases when converting limits here we will use the results of the inverse tangent or,
\[{\mbox{If }}\theta = {\tan ^{ - 1}}\left( x \right)\,\,{\mbox{then}}\,\, - \frac{\pi }{2} < \theta < \frac{\pi }{2}\]So, in this range of \(\theta \) secant is positive and so we can drop the absolute value bars.
Here is the integral,
\[\begin{align*}\int_{{\,0}}^{{\,\frac{1}{6}}}{{\frac{{{x^5}}}{{{{\left( {36{x^2} + 1} \right)}^{\frac{3}{2}}}}}\,dx}} & = \int_{{\,0}}^{{\,\frac{\pi }{4}}}{{\frac{{\frac{1}{{7776}}{{\tan }^5}\theta }}{{{{\sec }^3}\theta }}\,\left( {\frac{1}{6}{{\sec }^2}\theta } \right)d\theta }}\\ & = \frac{1}{{46656}}\int_{{\,0}}^{{\,\frac{\pi }{4}}}{{\frac{{{{\tan }^5}\theta }}{{\sec \theta }}d\theta }}\end{align*}\]There are several ways to proceed from this point. Normally with an odd exponent on the tangent we would strip one of them out and convert to secants. However, that would require that we also have a secant in the numerator which we don’t have. Therefore, it seems like the best way to do this one would be to convert the integrand to sines and cosines.
\[\begin{align*}\int_{{\,0}}^{{\,\frac{1}{6}}}{{\frac{{{x^5}}}{{{{\left( {36{x^2} + 1} \right)}^{\frac{3}{2}}}}}\,dx}} & = \frac{1}{{46656}}\int_{{\,0}}^{{\,\frac{\pi }{4}}}{{\frac{{{{\sin }^5}\theta }}{{{{\cos }^4}\theta }}d\theta }}\\ & = \frac{1}{{46656}}\int_{{\,0}}^{{\,\frac{\pi }{4}}}{{\frac{{{{\left( {1 - {{\cos }^2}\theta } \right)}^2}}}{{{{\cos }^4}\theta }}\sin \theta d\theta }}\end{align*}\]We can now use the substitution \(u = \cos \theta \) and we might as well convert the limits as well.
\[\begin{align*}\theta & = 0 & \hspace{0.75in} & u = \cos 0 = 1\\ \theta & = \frac{\pi }{4}& \hspace{0.75in} & u = \cos \frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\end{align*}\]The integral is then,
\[\begin{align*}\int_{{\,0}}^{{\,\frac{1}{6}}}{{\frac{{{x^5}}}{{{{\left( {36{x^2} + 1} \right)}^{\frac{3}{2}}}}}\,dx}} & = - \frac{1}{{46656}}\int_{{\,1}}^{{\,\frac{{\sqrt 2 }}{2}}}{{{u^{ - 4}} - 2{u^{ - 2}} + 1\,du}}\\ & = - \frac{1}{{46656}}\left. {\left( { - \frac{1}{{3{u^3}}} + \frac{2}{u} + u} \right)} \right|_1^{\frac{{\sqrt 2 }}{2}}\\ & = \frac{1}{{17496}} - \frac{{11\sqrt 2 }}{{279936}}\end{align*}\]Here is a summary for this final type of trig substitution.
Before proceeding with some more examples let’s discuss just how we knew to use the substitutions that we did in the previous examples.
The main idea was to determine a substitution that would allow us to reduce the two terms under the root that was always in the problem (more on this in a bit) into a single term and in doing so we were also able to easily eliminate the root. To do this we made use of the following formulas.
\[\begin{align*}25{x^2} - 4 & \hspace{0.25in} \Rightarrow \hspace{0.25in}{\sec ^2}\theta - 1 = {\tan ^2}\theta \\ 9 - {x^2} & \hspace{0.25in} \Rightarrow \hspace{0.25in}1 - {\sin ^2}\theta = {\cos ^2}\theta \\ 36{x^2} + 1 & \hspace{0.25in} \Rightarrow \hspace{0.25in}{\tan ^2}\theta + 1 = {\sec ^2}\theta \end{align*}\]If we step back a bit we can notice that the terms we reduced look like the trig identities we used to reduce them in a vague way.
For instance, \(25{x^2} - 4\) is something squared (i.e. the \(25{x^2}\)) minus a number (i.e. the 4) and the left side of formula we used, \({\sec ^2}\theta - 1\), also follows this basic form. So, because the two look alike in a very vague way that suggests using a secant substitution for that problem. We can notice similar vague similarities in the other two cases as well.
If we keep this idea in mind we don’t need the “formulas” listed after each example to tell us which trig substitution to use and since we have to know the trig identities anyway to do the problems keeping this idea in mind doesn’t really add anything to what we need to know for the problems.
Once we’ve identified the trig function to use in the substitution the coefficient, the \(\frac{a}{b}\) in the formulas, is also easy to get. Just remember that in order to use the trig identities the coefficient of the trig function and the number in the identity must be the same, i.e. both 4 or 9, so that the trig identity can be used after we factor the common number out. What this means is that we need to “turn” the coefficient of the squared term into the constant number through our substitution.
So, in the first example we needed to “turn” the 25 into a 4 through our substitution. Remembering that we are eventually going to square the substitution that means we need to divide out by a 5 so the 25 will cancel out, upon squaring. Likewise, we’ll need to add a 2 to the substitution so the coefficient will “turn” into a 4 upon squaring. In other words, we would need to use the substitution that we did in the problem.
The same idea holds for the other two trig substitutions.
Notice as well that we could have used cosecant in the first case, cosine in the second case and cotangent in the third case. So, why didn’t we? Simply because of the differential work. Had we used these trig functions instead we would have picked up a minus sign in the differential that we’d need to keep track of. So, while these could be used they generally aren’t to avoid extra minus signs that we need to keep track of.
Next, let’s quickly address the fact that a root was in all of these problems. Note that the root is not required in order to use a trig substitution. Instead, the trig substitution gave us a really nice way of eliminating the root from the problem. In this section we will always be having roots in the problems, and in fact our summaries above all assumed roots, roots are not actually required in order use a trig substitution. We will be seeing an example or two of trig substitutions in integrals that do not have roots in the Integrals Involving Quadratics section.
Finally, let’s summarize up all the ideas with the trig substitutions we’ve discussed and again we will be using roots in the summary simply because all the integrals in this section will have roots and those tend to be the most likely places for using trig substitutions but again, are not required in order to use a trig substitution.
| Form | Looks Like | Substitution | Limit Assumptions |
|---|---|---|---|
| \[\sqrt {{b^2}{x^2} - {a^2}} \] | \[{\sec ^2}\theta - 1 = \tan^{2} \theta \] | \[x = \frac{a}{b}\sec \theta \] | \[0 \le \theta < \frac{\pi }{2},\,\,\frac{\pi }{2} < \theta \le \pi \] |
| \[\sqrt {{a^2} - {b^2}{x^2}} \] | \[1 - {\sin ^2}\theta = {\cos ^2}\theta \] | \[x = \frac{a}{b}\sin \theta \] | \[ - \frac{\pi }{2} \le \theta \le \frac{\pi }{2}\] |
| \[\sqrt {{a^2} + {b^2}{x^2}} \] | \[{\tan ^2}\theta + 1 = {\sec ^2}\theta \] | \[x = \frac{a}{b}\tan \theta \] | \[ - \frac{\pi }{2} < \theta < \frac{\pi }{2}\] |
Now, we have a couple of final examples to work in this section. Not all trig substitutions will just jump right out at us. Sometimes we need to do a little work on the integrand first to get it into the correct form and that is the point of the remaining examples.
In this case the quantity under the root doesn’t obviously fit into any of the cases we looked at above and in fact isn’t in the any of the forms we saw in the previous examples. Note however that if we complete the square on the quadratic we can make it look somewhat like the above integrals.
Remember that completing the square requires a coefficient of one in front of the \({x^2}\). Once we have that we take half the coefficient of the \(x\), square it, and then add and subtract it to the quantity. Here is the completing the square for this problem.
\[2\left( {{x^2} - 2x - \frac{7}{2}} \right) = 2\left( {{x^2} - 2x + 1 - 1 - \frac{7}{2}} \right) = 2\left( {{{\left( {x - 1} \right)}^2} - \frac{9}{2}} \right) = 2{\left( {x - 1} \right)^2} - 9\]So, the root becomes,
\[\sqrt {2{x^2} - 4x - 7} = \sqrt {2{{\left( {x - 1} \right)}^2} - 9} \]Now, this looks (very) vaguely like \({\sec ^2}\theta - 1\) (i.e. something squared minus a number) except we’ve got something more complicated in the squared term. That is okay we’ll still be able to do a secant substitution and it will work in pretty much the same way.
\[x - 1 = \frac{3}{{\sqrt 2 }}\sec \theta \hspace{0.25in}x = 1 + \frac{3}{{\sqrt 2 }}\sec \theta \hspace{0.25in}dx = \frac{3}{{\sqrt 2 }}\sec \theta \tan \theta \,d\theta \]Using this substitution the root reduces to,
\[\sqrt {2{x^2} - 4x - 7} = \sqrt {2{{\left( {x - 1} \right)}^2} - 9} = \sqrt {9{{\sec }^2}\theta - 9} = 3\sqrt {{{\tan }^2}\theta } = 3\left| {\tan \theta } \right| = 3\tan \theta \]Note we could drop the absolute value bars since we are doing an indefinite integral. Here is the integral.
\[\begin{align*}\int{{\frac{x}{{\sqrt {2{x^2} - 4x - 7} }}\,dx}} & = \int{{\frac{{1 + \frac{3}{{\sqrt 2 }}\sec \theta }}{{3\tan \theta }}\left( {\frac{3}{{\sqrt 2 }}\sec \theta \tan \theta } \right)\,d\theta }}\\ & = \int{{\frac{1}{{\sqrt 2 }}\sec \theta + \frac{3}{2}{{\sec }^2}\theta \,d\theta }}\\ & = \frac{1}{{\sqrt 2 }}\ln \left| {\sec \theta + \tan \theta } \right| + \frac{3}{2}\tan \theta + c\end{align*}\]And here is the right triangle for this problem.
\[\sec \theta = \frac{{\sqrt 2 \left( {x - 1} \right)}}{3}\hspace{0.5in}\tan \theta = \frac{{\sqrt {2{x^2} - 4x - 7} }}{3}\]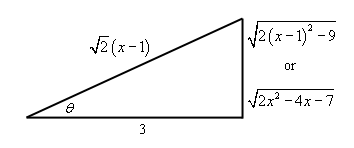
The integral is then,
\[\int{{\frac{x}{{\sqrt {2{x^2} - 4x - 7} }}\,dx}} = \frac{1}{{\sqrt 2 }}\ln \left| {\frac{{\sqrt 2 \left( {x - 1} \right)}}{3} + \frac{{\sqrt {2{x^2} - 4x - 7} }}{3}} \right| + \frac{{\sqrt {2{x^2} - 4x - 7} }}{2} + c\]This doesn’t look to be anything like the other problems in this section. However it is. To see this we first need to notice that,
\[{{\bf{e}}^{2x}} = {\left( {{{\bf{e}}^x}} \right)^2}\]Upon noticing this we can use the following standard Calculus I substitution.
\[u = {{\bf{e}}^x}\hspace{0.5in}du = {{\bf{e}}^x}\,dx\]We do need to be a little careful with the differential work however. We don’t have just an \({{\bf{e}}^x}\) out in front of the root. Instead we have an \({{\bf{e}}^{4x}}\). So, we’ll need to strip one of those out for the differential and then use the substitution on the rest. Here is the substitution work.
\[\begin{align*}\int{{{{\bf{e}}^{4x}}\sqrt {1 + {{\bf{e}}^{2x}}} \,dx}} & = \int{{{{\bf{e}}^{3x}}{{\bf{e}}^x}\sqrt {1 + {{\bf{e}}^{2x}}} \,dx}}\\ & = \int{{{{\left( {{{\bf{e}}^x}} \right)}^3}\sqrt {1 + {{\left( {{{\bf{e}}^x}} \right)}^2}} \,{{\bf{e}}^x}dx}} = \int{{{u^3}\sqrt {1 + {u^2}} \,du}}\end{align*}\]This is now a fairly obvious trig substitution (hopefully). The quantity under the root looks almost exactly like \(1 + {\tan ^2}\theta \) and so we can use a tangent substitution. Here is that work.
\[u = \tan \theta \hspace{0.25in}du = {\sec ^2}\theta \,d\theta \hspace{0.5in}\sqrt {1 + {u^2}} = \sqrt {1 + {{\tan }^2}\theta } = \sqrt {{{\sec }^2}\theta } = \left| {\sec \theta } \right|\]Because we are doing an indefinite integral we can assume secant is positive and drop the absolute value bars. Applying this substitution to the integral gives,
\[\int{{{{\bf{e}}^{4x}}\sqrt {1 + {{\bf{e}}^{2x}}} \,dx}} = \int{{{{\tan }^3}\theta \left( {\sec \theta } \right)\,\left( {{{\sec }^2}\theta } \right)d\theta }} = \int{{\tan^3 \theta \sec^3\theta d\theta }}\]We’ll finish this integral off in a bit. Before we get to that there is a “quicker” (although not super obvious) way of doing the substitutions above. Let’s cover that first then we’ll come back and finish working the integral.
We can notice that the \(u\) in the Calculus I substitution and the trig substitution are the same \(u\) and so we can combine them into the following substitution.
\[{{\bf{e}}^x} = \tan \theta \]We can then compute the differential. Just remember that all we do is differentiate both sides and then tack on \(dx\) or \(d\theta \) onto the appropriate side. Doing this gives,
\[{{\bf{e}}^x}\,dx = {\sec ^2}\theta \,d\theta \]With this substitution the square root becomes,
\[\sqrt {1 + {{\bf{e}}^{2x}}} = \sqrt {1 + {{\left( {{{\bf{e}}^x}} \right)}^2}} = \sqrt {1 + {{\tan }^2}\theta } = \sqrt {{{\sec }^2}\theta } = \left| {\sec \theta } \right| = \sec \theta \]Again, we can drop the absolute value bars because we are doing an indefinite integral. The integral then becomes,
\[\begin{align*}\int{{{{\bf{e}}^{4x}}\sqrt {1 + {{\bf{e}}^{2x}}} \,dx}} & = \int{{{{\bf{e}}^{3x}}{{\bf{e}}^x}\sqrt {1 + {{\bf{e}}^{2x}}} \,dx}}\\ & = \int{{{{\left( {{{\bf{e}}^x}} \right)}^3}\sqrt {1 + {{\bf{e}}^{2x}}} \,\left( {{{\bf{e}}^x}} \right)dx}}\\ & = \int{{{{\tan }^3}\theta \left( {\sec \theta } \right)}}\left( {{{\sec }^2}\theta } \right)\,d\theta = \int{{{{\tan }^3}\theta \,{{\sec }^3}\theta d\theta }}\end{align*}\]So, the same integral with less work. However, it does require that you be able to combine the two substitutions in to a single substitution. How you do this type of problem is up to you but if you don’t feel comfortable with the single substitution (and there’s nothing wrong if you don’t!) then just do the two individual substitutions. The single substitution method was given only to show you that it can be done so that those that are really comfortable with both kinds of substitutions can do the work a little quicker.
Now, let’s finish the integral work.
\[\begin{align*}\int{{{{\bf{e}}^{4x}}\sqrt {1 + {{\bf{e}}^{2x}}} \,dx}} & = \int{{{{\tan }^3}\theta \,{{\sec }^3}\theta d\theta }}\\ & = \int{{\left( {{{\sec }^2}\theta - 1} \right)}}{\sec ^2}\theta \,\sec \theta \tan \theta \,d\theta \hspace{0.5in}v = \sec \theta \\ & = \int{{{v^4} - {v^2}\,dv}}\\ & = \frac{1}{5}{\sec ^5}\theta - \frac{1}{3}{\sec ^3}\theta + c\end{align*}\]Here is the right triangle for this integral.
\[\tan \theta = \frac{{{{\bf{e}}^x}}}{1}\hspace{0.5in}\sec \theta = \frac{{\sqrt {1 + {{\bf{e}}^{2x}}} }}{1} = \sqrt {1 + {{\bf{e}}^{2x}}} \]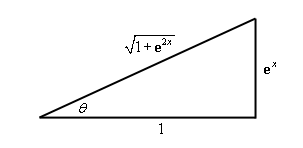
The integral is then,
\[\int{{{{\bf{e}}^{4x}}\sqrt {1 + {{\bf{e}}^{2x}}} \,dx}} = \frac{1}{5}{\left( {1 + {{\bf{e}}^{2x}}} \right)^{\frac{5}{2}}} - \frac{1}{3}{\left( {1 + {{\bf{e}}^{2x}}} \right)^{\frac{3}{2}}} + c\]This was a messy problem, but we will be seeing some of this type of integral in later sections on occasion so we needed to make sure you’d seen at least one like it.
So, as we’ve seen in the final two examples in this section some integrals that look nothing like the first few examples can in fact be turned into a trig substitution problem with a little work.