Section 11.3 : Dot Product
The next topic for discussion is that of the dot product. Let’s jump right into the definition of the dot product. Given the two vectors \(\vec a = \left\langle {{a_1},{a_2},{a_3}} \right\rangle \) and \(\vec b = \left\langle {{b_1},{b_2},{b_3}} \right\rangle \) the dot product is,
Sometimes the dot product is called the scalar product. The dot product is also an example of an inner product and so on occasion you may hear it called an inner product.
- \(\vec v = 5\vec i - 8\vec j,\,\,\vec w = \vec i + 2\vec j\)
- \(\vec a = \left\langle {0,3, - 7} \right\rangle ,\,\,\vec b = \left\langle {2,3,1} \right\rangle \)
Not much to do with these other than use the formula.
a \(\vec v\centerdot \vec w = 5 - 16 = - 11\)
b \(\vec a\centerdot \vec b = 0 + 9 - 7 = 2\)
Here are some properties of the dot product.
Properties
The proofs of these properties are mostly “computational” proofs and so we’re only going to do a couple of them and leave the rest to you to prove.
Proof of \(\vec u\centerdot \left( {\vec v + \vec w} \right) = \vec u\centerdot \vec v + \vec u\centerdot \vec w\)
We’ll start with the three vectors, \(\vec u = \left\langle {{u_1},{u_2}, \ldots ,{u_n}} \right\rangle \), \(\vec v = \left\langle {{v_1},{v_2}, \ldots ,{v_n}} \right\rangle \) and \(\vec w = \left\langle {{w_1},{w_2}, \ldots ,{w_n}} \right\rangle \) and yes we did mean for these to each have \(n\) components. The theorem works for general vectors so we may as well do the proof for general vectors.
Now, as noted above this is pretty much just a “computational” proof. What that means is that we’ll compute the left side and then do some basic arithmetic on the result to show that we can make the left side look like the right side. Here is the work.
\[\begin{align*}\vec u\centerdot \left( {\vec v + \vec w} \right) & = \left\langle {{u_1},{u_2}, \ldots ,{u_n}} \right\rangle \centerdot \left( {\left\langle {{v_1},{v_2}, \ldots ,{v_n}} \right\rangle + \left\langle {{w_1},{w_2}, \ldots ,{w_n}} \right\rangle } \right)\\ & = \left\langle {{u_1},{u_2}, \ldots ,{u_n}} \right\rangle \centerdot \left\langle {{v_1} + {w_1},{v_2} + {w_2}, \ldots ,{v_n} + {w_n}} \right\rangle \\ & = {{u_1}\left( {{v_1} + {w_1}} \right)+{u_2}\left( {{v_2} + {w_2}} \right)+ \ldots +{u_n}\left( {{v_n} + {w_n}} \right)} \\ & = {{u_1}{v_1} + {u_1}{w_1} + {u_2}{v_2} + {u_2}{w_2} + \ldots + {u_n}{v_n} + {u_n}{w_n}} \\ & = \left( {{u_1}{v_1} + {u_2}{v_2} + \ldots + {u_n}{v_n}} \right) + \left( {{u_1}{w_1} + {u_2}{w_2} + \ldots + {u_n}{w_n}} \right) \\ & = \left\langle {{u_1},{u_2}, \ldots ,{u_n}} \right\rangle \centerdot \left\langle {{v_1},{v_2}, \ldots ,{v_n}} \right\rangle + \left\langle {{u_1},{u_2}, \ldots ,{u_n}} \right\rangle \centerdot \left\langle {{w_1},{w_2}, \ldots ,{w_n}} \right\rangle \\ & = \vec u\centerdot \vec v + \vec u\centerdot \vec w\end{align*}\]Proof of : If \(\vec v\centerdot \vec v = 0\) then \(\vec v = \vec 0\)
This is a pretty simple proof. Let’s start with \(\vec v = \left\langle {{v_1},{v_2}, \ldots ,{v_n}} \right\rangle \) and compute the dot product.
\[\begin{align*}\vec v\centerdot \vec v & = \left\langle {{v_1},{v_2}, \ldots ,{v_n}} \right\rangle \centerdot \left\langle {{v_1},{v_2}, \ldots ,{v_n}} \right\rangle \\ & = v_1^2 + v_2^2 + \cdots + v_n^2\\ & = 0\end{align*}\]Now, since we know \(v_i^2 \ge 0\) for all \(i\) then the only way for this sum to be zero is to in fact have \(v_i^2 = 0\). This in turn however means that we must have \({v_i} = 0\) and so we must have had \(\vec v = \vec 0\).
There is also a nice geometric interpretation to the dot product. First suppose that \(\theta\) is the angle between \(\vec a\) and \(\vec b\) such that \(0 \le \theta \le \pi \) as shown in the image below.
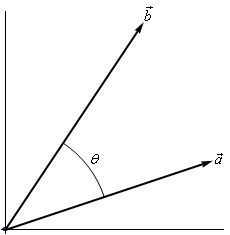
We can then have the following theorem.
Theorem
Proof
Let’s give a modified version of the sketch above.
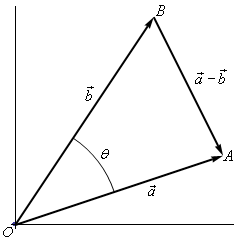
The three vectors above form the triangle AOB and note that the length of each side is nothing more than the magnitude of the vector forming that side.
The Law of Cosines tells us that,
\[{\left\| {\vec a - \vec b} \right\|^2} = {\left\| {\vec a} \right\|^2} + {\left\| {\vec b} \right\|^2} - 2\left\| {\vec a} \right\|\,\,\left\| {\vec b} \right\|\cos \theta \]Also using the properties of dot products we can write the left side as,
\[\begin{align*}{\left\| {\vec a - \vec b} \right\|^2} & = \left( {\vec a - \vec b} \right)\centerdot \left( {\vec a - \vec b} \right)\\ & = \vec a\centerdot \vec a - \vec a\centerdot \vec b - \vec b\centerdot \vec a + \vec b\centerdot \vec b\\ & = {\left\| {\vec a} \right\|^2} - 2\vec a\centerdot \vec b + {\left\| {\vec b} \right\|^2}\end{align*}\]Our original equation is then,
\[\begin{align*}{\left\| {\vec a - \vec b} \right\|^2} & = {\left\| {\vec a} \right\|^2} + {\left\| {\vec b} \right\|^2} - 2\left\| {\vec a} \right\|\,\,\left\| {\vec b} \right\|\cos \theta \\ {\left\| {\vec a} \right\|^2} - 2\vec a\centerdot \vec b + {\left\| {\vec b} \right\|^2} & = {\left\| {\vec a} \right\|^2} + {\left\| {\vec b} \right\|^2} - 2\left\| {\vec a} \right\|\,\,\left\| {\vec b} \right\|\cos \theta \\ - 2\vec a\centerdot \vec b & = - 2\left\| {\vec a} \right\|\,\,\left\| {\vec b} \right\|\cos \theta \\ \vec a\centerdot \vec b & = \left\| {\vec a} \right\|\,\,\left\| {\vec b} \right\|\cos \theta \end{align*}\]The formula from this theorem is often used not to compute a dot product but instead to find the angle between two vectors. Note as well that while the sketch of the two vectors in the proof is for two dimensional vectors the theorem is valid for vectors of any dimension (as long as they have the same dimension of course).
Let’s see an example of this.
We will need the dot product as well as the magnitudes of each vector.
\[\vec a\centerdot \vec b = - 22\hspace{0.25in}\hspace{0.25in}\left\| {\vec a} \right\| = \sqrt {26} \hspace{0.25in}\hspace{0.25in}\left\| {\vec b} \right\| = \sqrt {29} \]The angle is then,
\[\begin{align*}\cos \theta & = \frac{{\vec a\centerdot \vec b}}{{\left\| {\vec a} \right\|\,\,\left\| {\vec b} \right\|}} = \frac{{ - 22}}{{\sqrt {26} \sqrt {29} }} = - 0.8011927\\ & \\ \theta & = {\cos ^{ - 1}}\left( { - 0.8011927} \right) = 2.5{\mbox{ radians }} = 143.24 {\mbox{ degrees}}\end{align*}\]The dot product gives us a very nice method for determining if two vectors are perpendicular and it will give another method for determining when two vectors are parallel. Note as well that often we will use the term orthogonal in place of perpendicular.
Now, if two vectors are orthogonal then we know that the angle between them is 90 degrees. From \(\eqref{eq:eq2}\) this tells us that if two vectors are orthogonal then,
\[\vec a\centerdot \vec b = 0\]Likewise, if two vectors are parallel then the angle between them is either 0 degrees (pointing in the same direction) or 180 degrees (pointing in the opposite direction). Once again using \(\eqref{eq:eq2}\) this would mean that one of the following would have to be true.
\[\vec a\centerdot \vec b = \left\| {\vec a} \right\|\,\,\left\| {\vec b} \right\|\,\,\left( {\theta = 0^\circ } \right)\hspace{0.25in}{\mbox{OR}}\hspace{0.25in}\vec a\centerdot \vec b = - \left\| {\vec a} \right\|\,\,\left\| {\vec b} \right\|\,\,\left( {\theta = 180^\circ } \right)\]- \(\vec a = \left\langle {6, - 2, - 1} \right\rangle ,\,\,\vec b = \left\langle {2,5,2} \right\rangle \)
- \(\displaystyle \vec u = 2\vec i - \vec j,\,\,\vec v = - \frac{1}{2}\vec i + \frac{1}{4}\vec j\)
First get the dot product to see if they are orthogonal.
\[\vec a\centerdot \vec b = 12 - 10 - 2 = 0\]The two vectors are orthogonal.
b \(\displaystyle \vec u = 2\vec i - \vec j,\,\,\vec v = - \frac{1}{2}\vec i + \frac{1}{4}\vec j\) Show Solution
Again, let’s get the dot product first.
\[\vec u\centerdot \vec v = - 1 - \frac{1}{4} = - \frac{5}{4}\]So, they aren’t orthogonal. Let’s get the magnitudes and see if they are parallel.
\[\left\| {\vec u} \right\| = \sqrt 5 \hspace{0.25in}\left\| {\vec v} \right\| = \sqrt {\frac{5}{{16}}} = \frac{{\sqrt 5 }}{4}\]Now, notice that,
\[\vec u\centerdot \vec v = - \frac{5}{4} = - \sqrt 5 \left( {\frac{{\sqrt 5 }}{4}} \right) = - \left\| {\vec u} \right\|\,\,\left\| {\vec v} \right\|\]So, the two vectors are parallel.
There are several nice applications of the dot product as well that we should look at.
Projections
The best way to understand projections is to see a couple of sketches. So, given two vectors \(\vec a\) and \(\vec b\) we want to determine the projection of \(\vec b\) onto \(\vec a\). The projection is denoted by \({{\mathop{\rm proj}\nolimits} _{\vec a}}\vec b\). Here are a couple of sketches illustrating the projection.
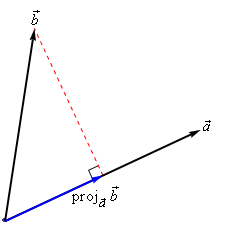
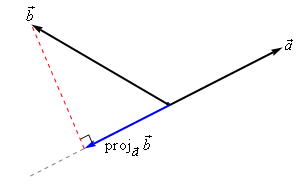
So, to get the projection of \(\vec b\) onto \(\vec a\) we drop straight down from the end of \(\vec b\)until we hit (and form a right angle) with the line that is parallel to \(\vec a\). The projection is then the vector that is parallel to \(\vec a\), starts at the same point both of the original vectors started at and ends where the dashed line hits the line parallel to \(\vec a\).
There is a nice formula for finding the projection of \(\vec b\) onto \(\vec a\). Here it is,
Note that we also need to be very careful with notation here. The projection of \(\vec a\) onto \(\vec b\)is given by
\[{{\mathop{\rm proj}\nolimits} _{\vec b}}\vec a = \frac{{\vec a\centerdot \vec b}}{{{{\left\| {\vec b} \right\|}^2}}}\vec b\]We can see that this will be a totally different vector. This vector is parallel to \(\vec b\), while \({{\mathop{\rm proj}\nolimits} _{\vec a}}\vec b\) is parallel to \(\vec a\). So, be careful with notation and make sure you are finding the correct projection.
Here’s an example.
We need the dot product and the magnitude of \(\vec a\).
\[\vec a\centerdot \vec b = 4\hspace{0.25in}\hspace{0.25in}{\left\| {\vec a} \right\|^2} = 5\]The projection is then,
\[\begin{align*}{{\mathop{\rm proj}\nolimits} _{\vec a}}\vec b & = \frac{{\vec a\centerdot \vec b}}{{{{\left\| {\vec a} \right\|}^2}}}\vec a\\ & = \frac{4}{5}\left\langle {1,0, - 2} \right\rangle \\ & = \left\langle {\frac{4}{5},0, - \frac{8}{5}} \right\rangle \end{align*}\]For comparison purposes let’s do it the other way around as well.
We need the dot product and the magnitude of \(\vec b\).
\[\vec a\centerdot \vec b = 4\hspace{0.25in}\hspace{0.25in}{\left\| {\vec b} \right\|^2} = 6\]The projection is then,
\[\begin{align*}{{\mathop{\rm proj}\nolimits} _{\vec b}}\vec a & = \frac{{\vec a\centerdot \vec b}}{{{{\left\| {\vec b} \right\|}^2}}}\vec b\\ & = \frac{4}{6}\left\langle {2,1, - 1} \right\rangle \\ & = \left\langle {\frac{4}{3},\frac{2}{3}, - \frac{2}{3}} \right\rangle \end{align*}\]As we can see from the previous two examples the two projections are different so be careful.
Direction Cosines
This application of the dot product requires that we be in three dimensional space unlike all the other applications we’ve looked at to this point.
Let’s start with a vector, \(\vec a\), in three dimensional space. This vector will form angles with the \(x\)-axis (a ), the \(y\)-axis (b ), and the \(z\)-axis (g ). These angles are called direction angles and the cosines of these angles are called direction cosines.
Here is a sketch of a vector and the direction angles.
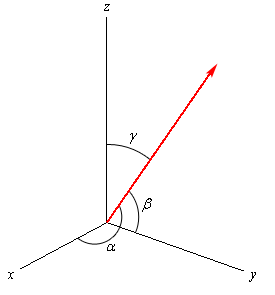
The formulas for the direction cosines are,
where \(\vec i\), \(\vec j\) and \(\vec k\) are the standard basis vectors.
Let’s verify the first dot product above. We’ll leave the rest to you to verify.
\[\vec a\centerdot \,\vec i = \left\langle {{a_1},{a_2},{a_3}} \right\rangle \centerdot \left\langle {1,0,0} \right\rangle = {a_1}\]Here are a couple of nice facts about the direction cosines.
- The vector \(\vec u = \left\langle {\cos \alpha ,\cos \beta ,\cos \gamma } \right\rangle \) is a unit vector.
- \({\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\gamma = 1\)
- \(\vec a = \left\| {\vec a} \right\|\left\langle {\cos \alpha ,\cos \beta ,\cos \gamma } \right\rangle \)
Let’s do a quick example involving direction cosines.
We will need the magnitude of the vector.
\[\left\| {\vec a} \right\| = \sqrt {4 + 1 + 16} = \sqrt {21} \]The direction cosines and angles are then,
\[\begin{align*}\cos \alpha & = \frac{2}{{\sqrt {21} }}\hspace{0.25in}\hspace{0.25in}\alpha = 1.119{\mbox{ radians}} = 64.123{\mbox{ degrees}}\\ \cos \beta & = \frac{1}{{\sqrt {21} }}\hspace{0.25in}\hspace{0.25in}\beta = 1.351{\mbox{ radians}} = 77.396{\mbox{ degrees}}\\ \cos \gamma & = \frac{{ - 4}}{{\sqrt {21} }}\hspace{0.25in}\hspace{0.25in}\gamma = 2.632{\mbox{ radians}} = 150.794{\mbox{ degrees}}\end{align*}\]