Section 1.13 : Solving Inequalities

Solve each of the following inequalities. Show All Solutions Hide All Solutions

1. \({x^2} - 10 > 3x\)
   Show Solution

   To solve a polynomial inequality we get a zero on one side of the inequality, factor and then determine where the other side is zero.

   \[{x^2} - 10 > 3x\quad \Rightarrow \quad {x^2} - 3x - 10 > 0\quad \Rightarrow \quad \left( {x - 5} \right)\left( {x + 2} \right) > 0\]

   So, once we move everything over to the left side and factor we can see that the left side will be zero at \(x = 5\) and \(x = - 2\). These numbers are NOT solutions (since we only looking for values that will make the equation positive) but are useful to finding the actual solution.

   To find the solution to this inequality we need to recall that polynomials are nice smooth functions that have no breaks in them. This means that as we are moving across the number line (in any direction) if the value of the polynomial changes sign (say from positive to negative) then it MUST go through zero!

   So, that means that these two numbers (\(x = 5\) and \(x = - 2\)) are the ONLY places where the polynomial can change sign. The number line is then divided into three regions. In each region if the inequality is satisfied by one point from that region then it is satisfied for ALL points in that region. If this wasn’t true (i.e it was positive at one point in region and negative at another) then it must also be zero somewhere in that region, but that can’t happen as we’ve already determined all the places where the polynomial can be zero! Likewise, if the inequality isn’t satisfied for some point in that region that it isn’t satisfied for ANY point in that region.

   This means that all we need to do is pick a test point from each region (that are easy to work with, i.e. small integers if possible) and plug it into the inequality. If the test point satisfies the inequality then every point in that region does and if the test point doesn’t satisfy the inequality then no point in that region does.

   One final note here about this. I’ve got three versions of the inequality above. You can plug the test point into any of them, but it’s usually easiest to plug the test points into the factored form of the inequality. So, if you trust your factoring capabilities that’s the one to use. However, if you HAVE made a mistake in factoring, then you may end up with the incorrect solution if you use the factored form for testing. It’s a trade-off. The factored form is, in many cases, easier to work with, but if you’ve made a mistake in factoring you may get the incorrect solution.

   So, here’s the number line and tests that I used for this problem.

   

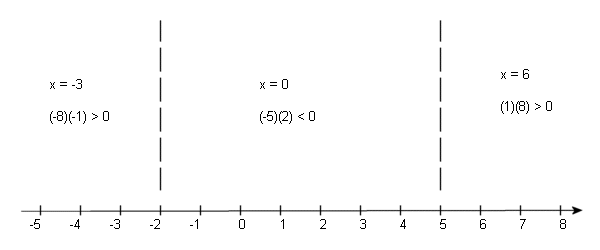
   From this we see that the solution to this inequality is \( - \infty < x < - 2\) and \(5 < x < \infty \). In interval notation this would be \(\left( { - \infty , - 2} \right)\) and \(\left( {5,\infty } \right)\). You’ll notice that the endpoints were not included in the solution for this. Pay attention to the original inequality when writing down the answer for these. Since the inequality was a strict inequality, we don’t include the endpoints since these are the points that make both sides of the inequality equal!

2. \({x^4} + 4{x^3} - 12{x^2} \le 0\)
   Show Solution

   We’ll do the same with this problem as the last problem.

   \[{x^4} + 4{x^3} - 12{x^2} \le 0\quad \Rightarrow \quad {x^2}\left( {{x^2} + 4x - 12} \right) \le 0\quad \Rightarrow \quad {x^2}\left( {x + 6} \right)\left( {x - 2} \right) \le 0\]

   In this case after factoring we can see that the left side will be zero at \(x = - 6\), \(x = 0\) and \(x = 2\).

   

   From this number line the solution to the inequality is \( - 6 \le x \le 2\) or [-6,2]. Do not get locked into the idea that the intervals will alternate as solutions as they did in the first problem. Also, notice that in this case the inequality was less than OR EQUAL TO, so we did include the endpoints in our solution.

3. \(3{x^2} - 2x - 11 > 0\)
   Show Solution

   This one is a little different, but not really more difficult. The quadratic doesn’t factor so we’ll need to use the quadratic formula to solve for where it is zero. Doing this gives

   \[x = \frac{{1 \pm \sqrt {34} }}{3}\]

   Reducing to decimals this is \(x = 2.27698\) and \(x = - 1.61032\). From this point on it’s identical to the previous two problems. In the number line below the dashed lines are at the approximate values of the two numbers above and the inequalities show the value of the quadratic evaluated at the test points shown.

   

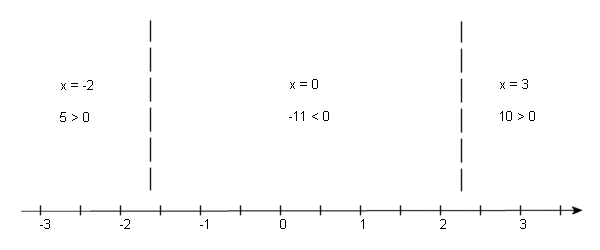
   From the number line above we see that the solution is \(\left( { - \infty ,\frac{{1 - \sqrt {34} }}{3}} \right)\) and \(\left( {\frac{{1 + \sqrt {34} }}{3},\infty } \right)\).

4. \(\displaystyle \frac{{x - 3}}{{x + 2}} \ge 0\)
   Show Solution

   The process for solving inequalities that involve rational functions is nearly identical to solving inequalities that involve polynomials. Just like polynomial inequalities, rational inequalities can change sign where the rational expression is zero. However, they can also change sign at any point that produces a division by zero error in the rational expression. A good example of this is the rational expression \(\frac{1}{x}\). Clearly, there is division by zero at \(x = 0\) and to the right of \(x = 0\)the expression is positive and to the left of \(x = 0\)the expression is negative.

   It’s also important to note that a rational expression will only be zero for values of \(x\) that make the numerator zero.

   So, what we need to do is first get a zero on one side of the inequality so we can use the above information. For this problem that has already been done. Now, determine where the numerator is zero (since the whole expression will be zero there) and where the denominator is zero (since we will get division by zero there).

   At this point the process is identical to polynomial inequalities with one exception when we go to write down the answer. The points found above will divide the number line into regions in which the inequality will either always be true or always be false. So, pick test points from each region, test them in the inequality and get the solution from the results.

   For this problem the numerator will be zero at \(x = 3\) and the denominator will be zero at \(x = - 2\). The number line, along with the tests is shown below.

   

   So, from this number line it looks like the two outer regions will satisfy the inequality. We need to be careful with the endpoints however. We will include \(x = 3\) because this will make the rational expression zero and so will be part of the solution. On the other hand, \(x = - 2\) will give division by zero and so MUST be excluded from the solution since division by zero is never allowed.

   The solution to this inequality is \( - \infty < x < - 2\) and \(3 \le x < \infty \) OR \(( - \infty - 2)\)and \([3,\infty )\), depending on if you want inequality for the solution or intervals for the solution.

5. \(\displaystyle \frac{{{x^2} - 3x - 10}}{{x - 1}} < 0\)
   Show Solution

   We already have a zero on one side of the inequality so first factor the numerator so we can get the points where the numerator will be zero.

   \[\frac{{\left( {x - 5} \right)\left( {x + 2} \right)}}{{x - 1}} < 0\]

   So, the numerator will be zero at \(x = - 2\) and \(x = 5\). The denominator will be zero at \(x = 1\). The number line for this inequality is below.

   

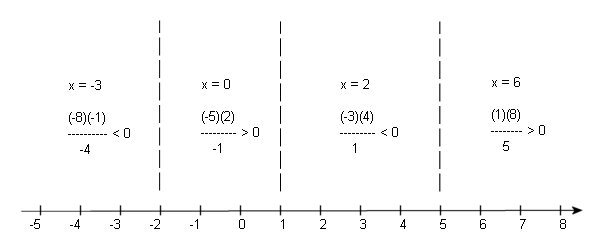
   In this case we won’t include any endpoints in the solution since they either give division by zero or make the expression zero and we want strictly less than zero for this problem.

   The solution is then \(( - \infty , - 2)\) and \((1,5)\).

6. \(\displaystyle \frac{{2x}}{{x + 1}} \ge 3\)
   Show Solution

   We need to be a little careful with this one. In this case we need to get zero on one side of the inequality. This is easy enough to do. All we need to do is subtract 3 from both sides. This gives

   \[\begin{align*}\frac{{2x}}{{x + 1}} - 3 & \ge 0\\ \frac{{2x - 3\left( {x + 1} \right)}}{{x + 1}} & \ge 0\\ \frac{{ - x - 3}}{{x + 1}} & \ge 0\end{align*}\]

   Notice that I also combined everything into a single rational expression. You will always want to do this. If you don’t do this it can be difficult to determine where the rational expression is zero. So, once we’ve gotten it into a single expression it’s easy to see that the numerator will be zero at \(x = - 3\) and the denominator will be zero at \(x = - 1\). The number line for this problem is below.

   

   The solution in this case is \([ - 3, - 1)\). We don’t include the -1 because this is where the solution is zero, but we do include the -3 because this makes the expression zero.