Calculus I - Derivatives of Inverse Trig Functions

Show Mobile Notice Show All Notes Hide All Notes

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best views in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (should be able to scroll to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 3.7 : Derivatives of Inverse Trig Functions

In this section we are going to look at the derivatives of the inverse trig functions. In order to derive the derivatives of inverse trig functions we’ll need the formula from the last section relating the derivatives of inverse functions. If $f\left( x \right)$ and $g\left( x \right)$ are inverse functions then,

\[g'\left( x \right) = \frac{1}{{f'\left( {g\left( x \right)} \right)}}\]

Recall as well that two functions are inverses if $f\left( {g\left( x \right)} \right) = x$ and $g\left( {f\left( x \right)} \right) = x$.

We’ll go through inverse sine, inverse cosine and inverse tangent in detail here and leave the other three to you to derive if you’d like to.

Inverse Sine

Let’s start with inverse sine. Here is the definition of the inverse sine.

\[y = {\sin ^{ - 1}}x\hspace{0.5in} \Leftrightarrow \hspace{0.5in}\sin y = x\hspace{0.25in}{\mbox{for}}\,\,\,\,\,\,\,\,\, - \frac{\pi }{2} \le y \le \frac{\pi }{2}\]

So, evaluating an inverse trig function is the same as asking what angle (i.e. $y$) did we plug into the sine function to get $x$. The restrictions on $y$ given above are there to make sure that we get a consistent answer out of the inverse sine. We know that there are in fact an infinite number of angles that will work and we want a consistent value when we work with inverse sine. Using the range of angles above gives all possible values of the sine function exactly once. If you’re not sure of that sketch out a unit circle and you’ll see that that range of angles (the $y$’s) will cover all possible values of sine.

Note as well that since $ - 1 \le \sin \left( y \right) \le 1$ we also have $ - 1 \le x \le 1$.

Let’s work a quick example.

Example 1 Evaluate $\displaystyle {\sin ^{ - 1}}\left( {\frac{1}{2}} \right)$

Show Solution

So, we are really asking what angle $y$ solves the following equation.

\[\sin \left( y \right) = \frac{1}{2}\]

and we are restricted to the values of $y$ above.

From a unit circle we can quickly see that $y = \frac{\pi }{6}$.

We have the following relationship between the inverse sine function and the sine function.

\[\sin \left( {{{\sin }^{ - 1}}x} \right) = x\hspace{0.5in}{\sin ^{ - 1}}\left( {\sin x} \right) = x\]

In other words they are inverses of each other. This means that we can use the fact above to find the derivative of inverse sine. Let’s start with,

\[f\left( x \right) = \sin x\hspace{0.5in}g\left( x \right) = {\sin ^{ - 1}}x\]

Then,

\[g'\left( x \right) = \frac{1}{{f'\left( {g\left( x \right)} \right)}} = \frac{1}{{\cos \left( {{{\sin }^{ - 1}}x} \right)}}\]

This is not a very useful formula. Let’s see if we can get a better formula. Let’s start by recalling the definition of the inverse sine function.

\[y = {\sin ^{ - 1}}\left( x \right)\hspace{0.5in} \Rightarrow \hspace{0.5in}x = \sin \left( y \right)\]

Using the first part of this definition the denominator in the derivative becomes,

\[\cos \left( {{{\sin }^{ - 1}}x} \right) = \cos \left( y \right)\]

Now, recall that

\[{\cos ^2}y + {\sin ^2}y = 1\hspace{0.5in} \Rightarrow \hspace{0.5in}\cos y = \sqrt {1 - {{\sin }^2}y} \]

Using this, the denominator is now,

\[\cos \left( {{{\sin }^{ - 1}}x} \right) = \cos \left( y \right) = \sqrt {1 - {{\sin }^2}y} \]

Now, use the second part of the definition of the inverse sine function. The denominator is then,

\[\cos \left( {{{\sin }^{ - 1}}x} \right) = \sqrt {1 - {{\sin }^2}y} = \sqrt {1 - {x^2}} \]

Putting all of this together gives the following derivative.

\[\frac{d}{{dx}}\left( {{{\sin }^{ - 1}}x} \right) = \frac{1}{{\sqrt {1 - {x^2}} }}\]

Inverse Cosine

Now let’s take a look at the inverse cosine. Here is the definition for the inverse cosine.

\[y = {\cos ^{ - 1}}x\hspace{0.5in} \Leftrightarrow \hspace{0.5in}\cos y = x\hspace{0.25in}{\mbox{for}}\,\,\,\,\,\,\,\,\,0 \le y \le \pi \]

As with the inverse sine we’ve got a restriction on the angles, $y$, that we get out of the inverse cosine function. Again, if you’d like to verify this a quick sketch of a unit circle should convince you that this range will cover all possible values of cosine exactly once. Also, we also have $ - 1 \le x \le 1$ because $ - 1 \le \cos \left( y \right) \le 1$.

Example 2 Evaluate $\displaystyle {\cos ^{ - 1}}\left( { - \frac{{\sqrt 2 }}{2}} \right)$.

Show Solution

As with the inverse sine we are really just asking the following.

\[\cos y = - \frac{{\sqrt 2 }}{2}\]

where $y$ must meet the requirements given above. From a unit circle we can see that we must have $y = \frac{{3\pi }}{4}$.

The inverse cosine and cosine functions are also inverses of each other and so we have,

\[\cos \left( {{{\cos }^{ - 1}}x} \right) = x\hspace{0.5in}{\cos ^{ - 1}}\left( {\cos x} \right) = x\]

To find the derivative we’ll do the same kind of work that we did with the inverse sine above. If we start with

\[f\left( x \right) = \cos x\hspace{0.5in}g\left( x \right) = {\cos ^{ - 1}}x\]

then,

\[g'\left( x \right) = \frac{1}{{f'\left( {g\left( x \right)} \right)}} = \frac{1}{{ - \sin \left( {{{\cos }^{ - 1}}x} \right)}}\]

Simplifying the denominator here is almost identical to the work we did for the inverse sine and so isn’t shown here. Upon simplifying we get the following derivative.

\[\frac{d}{{dx}}\left( {{{\cos }^{ - 1}}x} \right) = - \frac{1}{{\sqrt {1 - {x^2}} }}\]

So, the derivative of the inverse cosine is nearly identical to the derivative of the inverse sine. The only difference is the negative sign.

Inverse Tangent

Here is the definition of the inverse tangent.

\[y = {\tan ^{ - 1}}x\hspace{0.5in} \Leftrightarrow \hspace{0.5in}\tan y = x\hspace{0.25in}{\mbox{for}}\,\,\,\,\,\,\,\,\, - \frac{\pi }{2} < y < \frac{\pi }{2}\]

Again, we have a restriction on $y$, but notice that we can’t let $y$ be either of the two endpoints in the restriction above since tangent isn’t even defined at those two points. To convince yourself that this range will cover all possible values of tangent do a quick sketch of the tangent function and we can see that in this range we do indeed cover all possible values of tangent. Also, in this case there are no restrictions on $x$ because tangent can take on all possible values.

Example 3 Evaluate ${\tan ^{ - 1}}1$.

Show Solution

Here we are asking,

\[\tan y = 1\]

where $y$ satisfies the restrictions given above. From a unit circle we can see that $y = \frac{\pi }{4}$.

Because there is no restriction on $x$ we can ask for the limits of the inverse tangent function as $x$ goes to plus or minus infinity. To do this we’ll need the graph of the inverse tangent function. This is shown below.

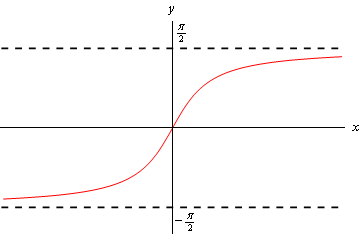
$Graph of $y={{\tan }^{-1}}\left( x \right)$. The graph starts on the left at the horizontal asymptote at $y=-\frac{\pi }{2}$ and increases going through (0,0) and then approaching another horizontal asymptote at $y=\frac{\pi }{2}$.$

From this graph we can see that

\[\mathop {\lim }\limits_{x \to \infty } {\tan ^{ - 1}}x = \frac{\pi }{2}\hspace{0.5in}\hspace{0.25in}\mathop {\lim }\limits_{x \to - \infty } {\tan ^{ - 1}}x = - \frac{\pi }{2}\]

The tangent and inverse tangent functions are inverse functions so,

\[\tan \left( {{{\tan }^{ - 1}}x} \right) = x\hspace{0.5in}{\tan ^{ - 1}}\left( {\tan x} \right) = x\]

Therefore, to find the derivative of the inverse tangent function we can start with

\[f\left( x \right) = \tan x\hspace{0.5in}g\left( x \right) = {\tan ^{ - 1}}x\]

We then have,

\[g'\left( x \right) = \frac{1}{{f'\left( {g\left( x \right)} \right)}} = \frac{1}{{{{\sec }^2}\left( {{{\tan }^{ - 1}}x} \right)}}\]

Simplifying the denominator is similar to the inverse sine, but different enough to warrant showing the details. We’ll start with the definition of the inverse tangent.

\[y = {\tan ^{ - 1}}x\hspace{0.5in} \Rightarrow \hspace{0.5in}\tan y = x\]

The denominator is then,

\[{\sec ^2}\left( {{{\tan }^{ - 1}}x} \right) = {\sec ^2}y\]

Now, if we start with the fact that

\[{\cos ^2}y + {\sin ^2}y = 1\]

and divide every term by cos² $y$ we will get,

\[1 + {\tan ^2}y = {\sec ^2}y\]

The denominator is then,

\[{\sec ^2}\left( {{{\tan }^{ - 1}}x} \right) = {\sec ^2}y = 1 + {\tan ^2}y\]

Finally using the second portion of the definition of the inverse tangent function gives us,

\[{\sec ^2}\left( {{{\tan }^{ - 1}}x} \right) = 1 + {\tan ^2}y = 1 + {x^2}\]

The derivative of the inverse tangent is then,

\[\frac{d}{{dx}}\left( {{{\tan }^{ - 1}}x} \right) = \frac{1}{{1 + {x^2}}}\]

There are three more inverse trig functions but the three shown here the most common ones. Formulas for the remaining three could be derived by a similar process as we did those above. Here are the derivatives of all six inverse trig functions.

\[\begin{array}{ll}\displaystyle \frac{d}{{dx}}\left( {{{\sin }^{ - 1}}x} \right) = \frac{1}{{\sqrt {1 - {x^2}} }} & \hspace{1.0in}\displaystyle \frac{d}{{dx}}\left( {{{\cos }^{ - 1}}x} \right) = - \frac{1}{{\sqrt {1 - {x^2}} }}\\ \displaystyle \frac{d}{{dx}}\left( {{{\tan }^{ - 1}}x} \right) = \frac{1}{{1 + {x^2}}} & \hspace{1.0in}\displaystyle \frac{d}{{dx}}\left( {{{\cot }^{ - 1}}x} \right) = - \frac{1}{{1 + {x^2}}}\\ \displaystyle \frac{d}{{dx}}\left( {{{\sec }^{ - 1}}x} \right) = \frac{1}{{\left| x \right|\sqrt {{x^2} - 1} }} & \hspace{1.0in}\displaystyle \frac{d}{{dx}}\left( {{{\csc }^{ - 1}}x} \right) = - \frac{1}{{\left| x \right|\sqrt {{x^2} - 1} }}\end{array}\]

We should probably now do a couple of quick derivatives here before moving on to the next section.

Example 4 Differentiate the following functions.

$f\left( t \right) = 4{\cos ^{ - 1}}\left( t \right) - 10{\tan ^{ - 1}}\left( t \right)$
$y = \sqrt z \, {\sin ^{ - 1}}\left( z \right)$

Show All Solutions Hide All Solutions

a $f\left( t \right) = 4{\cos ^{ - 1}}\left( t \right) - 10{\tan ^{ - 1}}\left( t \right)$ Show Solution

Not much to do with this one other than differentiate each term.

\[f'\left( t \right) = - \frac{4}{{\sqrt {1 - {t^2}} }} - \frac{{10}}{{1 + {t^2}}}\]

b $y = \sqrt z \, {\sin ^{ - 1}}\left( z \right)$ Show Solution

Don’t forget to convert the radical to fractional exponents before using the product rule.

\[y' = \frac{1}{2}{z^{ - \frac{1}{2}}}{\sin ^{ - 1}}\left( z \right) + \frac{{\sqrt z }}{{\sqrt {1 - {z^2}} }}\]

Alternate Notation

There is some alternate notation that is used on occasion to denote the inverse trig functions. This notation is,

\[\begin{array}{ll}{\sin ^{ - 1}}x = \arcsin x & \hspace{1.0in}{\cos ^{ - 1}}x = \arccos x\\ {\tan ^{ - 1}}x = \arctan x & \hspace{1.0in}{\cot ^{ - 1}}x = {\mbox{arccot }}x\\ {\sec ^{ - 1}}x = {\mathop{\rm arcsec}\nolimits} \,x & \hspace{1.0in}{\csc ^{ - 1}}x = {\mathop{\rm arccsc}\nolimits} \,x\end{array}\]