Calculus I - One-Sided Limits (Assignment Problems)

Show Mobile Notice Show All Notes Hide All Notes

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Assignment Problems Notice

Please do not email me to get solutions and/or answers to these problems. I will not give them out under any circumstances nor will I respond to any requests to do so. The intent of these problems is for instructors to use them for assignments and having solutions/answers easily available defeats that purpose.

If you are looking for some problems with solutions you can find some by clicking on the "Practice Problems" link above.

Section 2.3 : One-Sided Limits

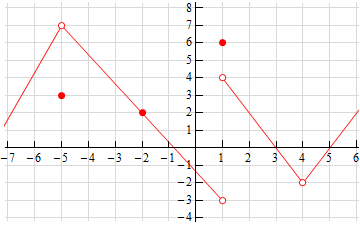
Below is the graph of $f\left( x \right)$. For each of the given points determine the value of $f\left( a \right)$, $\mathop {\lim }\limits_{x \to {a^{\, - }}} f\left( x \right)$, $\mathop {\lim }\limits_{x \to {a^{\, + }}} f\left( x \right)$, and $\mathop {\lim }\limits_{x \to a} f\left( x \right)$. If any of the quantities do not exist clearly explain why.
1. $a = - 5$
2. $a = - 2$
3. $a = 1$
4. $a = 4$
$This graph consists of two V shaped portions. The first portion is in the domain $-7 \le x < 1$. Its point is at (-5,7) – this is an open dot, and opens downwards. There is a closed dot at (-5,3) and at (-2,2). The graph ends on the right at an open dot at (1,-3). The second portion is in the domain $1 < x \le 6$. Its point is at (4,-2) – this is an open dot, and opens upwards. The graph starts at an open dot at (1,4) and there is a closed dot at (1,6).$
Below is the graph of $f\left( x \right)$. For each of the given points determine the value of $f\left( a \right)$, $\mathop {\lim }\limits_{x \to {a^{\, - }}} f\left( x \right)$, $\mathop {\lim }\limits_{x \to {a^{\, + }}} f\left( x \right)$, and $\mathop {\lim }\limits_{x \to a} f\left( x \right)$. If any of the quantities do not exist clearly explain why.
1. $a = - 1$
2. $a = 1$
3. $a = 3$
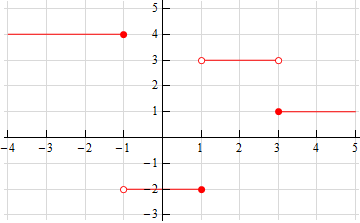
$This graph consists of four horizontal line segments. The first is in the domain $x < -1$ and is at y=4. It ends at a closed dot of (-1,4). The second is in the domain $-1 < x < \le 1$ and is at y=-2. It starts at an open dot at (-1,-2) and ends at a closed dot at (1,-2). The third is in the domain $1 < x < 3$ and is at y=3. It starts at an open dot of (1,3) and ends at an open dot of (3,3). The final segment is in the domain $x>3$ and is at y=1. It starts with a closed dot at (3,1).$
Below is the graph of $f\left( x \right)$. For each of the given points determine the value of $f\left( a \right)$, $\mathop {\lim }\limits_{x \to {a^{\, - }}} f\left( x \right)$, $\mathop {\lim }\limits_{x \to {a^{\, + }}} f\left( x \right)$, and $\mathop {\lim }\limits_{x \to a} f\left( x \right)$. If any of the quantities do not exist clearly explain why.
1. $a = - 3$
2. $a = - 1$
3. $a = 1$
4. $a = 2$
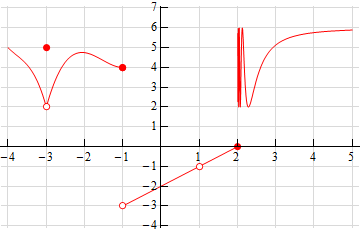
$This graph consists of four segments. The first is in the domain $x < -3$. This segment is a decreasing function that starts at (-4,5) and ends at an open dot at (-3,2). There is also a closed dot at (-3,5). The second segment is in the domain $-3 < x \le -1$. It starts with an open dot at (-3,2) and increases until approximately (-2.2, 4.8) and then decreases until it ends at a closed dot at (-1,4). The third segment is in the domain $-1 < x < \le 2$. It starts with a closed dot at (-1,-3) has an open dot at (1,-1) and ends at a closed dot at (2,0). The final segment is in the domain $x > 2$. The graph in the segment is an oscillating function that oscillates faster and faster as it approaches x = 2 from the right and the oscillation slows down as it moves away from x=2.$
Sketch a graph of a function that satisfies each of the following conditions. \[\mathop {\lim }\limits_{x \to {1^{\, - }}} f\left( x \right) = - 2\hspace{0.75in}\mathop {\lim }\limits_{x \to {1^{\, + }}} f\left( x \right) = 3\hspace{0.75in}f\left( 1 \right) = 6\]
Sketch a graph of a function that satisfies each of the following conditions. \[\mathop {\lim }\limits_{x \to \, - {3^{\, - }}} f\left( x \right) = 1\hspace{0.75in}\mathop {\lim }\limits_{x \to \, - {3^{\, + }}} f\left( x \right) = 1\hspace{0.75in}f\left( { - 3} \right) = 4\]
Sketch a graph of a function that satisfies each of the following conditions. \[\begin{array}{cll}\mathop {\lim }\limits_{x \to \, - {5^{\, - }}} f\left( x \right) = - 1\hspace{0.5in} & \mathop {\lim }\limits_{x \to \, - {5^{\, + }}} f\left( x \right) = 7\hspace{0.5in} & f\left( { - 5} \right) = 4\\ \mathop {\lim }\limits_{x \to 4} f\left( x \right) = 6\hspace{0.5in} & f\left( 4 \right)\,\,\,{\mbox{does not exist}} & \end{array}\]
Explain in your own words what each of the following equations mean. \[\mathop {\lim }\limits_{x \to {8^{\, - }}} f\left( x \right) = 3\hspace{0.75in}\mathop {\lim }\limits_{x \to {8^{\, + }}} f\left( x \right) = - 1\]
Suppose we know that $\mathop {\lim }\limits_{x \to \, - 7} f\left( x \right) = 18$. If possible, determine the value of $\mathop {\lim }\limits_{x \to \, - 7{\,^ - }} f\left( x \right)$ and the value of $\mathop {\lim }\limits_{x \to \, - 7{\,^ + }} f\left( x \right)$. If it is not possible to determine one or both of these values explain why not.
Suppose we know that $f\left( 6 \right) = - 53$. If possible, determine the value of $\mathop {\lim }\limits_{x \to \,6{\,^ - }} f\left( x \right)$ and the value of $\mathop {\lim }\limits_{x \to \,6{\,^ + }} f\left( x \right)$. If it is not possible to determine one or both of these values explain why not.