Mobile Notice
You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.
Assignment Problems Notice
Please do not email me to get solutions and/or answers to these problems. I will not give them out under any circumstances nor will I respond to any requests to do so. The intent of these problems is for instructors to use them for assignments and having solutions/answers easily available defeats that purpose.
If you are looking for some problems with solutions you can find some by clicking on the "Practice Problems" link above.
If you are looking for some problems with solutions you can find some by clicking on the "Practice Problems" link above.
Section 3.11 : Related Rates
- In the following assume that \(x\) and \(y\) are both functions of \(t\). Given \(x = 3\), \(y = 2\) and \(y' = 7\) determine \(x'\) for the following equation. \[{x^3} - {y^4} = {x^2}y - 7\]
- In the following assume that \(x\) and \(y\) are both functions of \(t\). Given \(x = {\textstyle{\pi \over 6}}\), \(y = - 4\) and \(x' = 12\) determine \(y'\) for the following equation. \[{x^2}\left( {{y^2} - 16} \right) - 6\cos \left( {2x} \right) = 1 + y\]
- In the following assume that \(x\), \(y\) and \(z\) are all functions of \(t\). Given \(x = - 1\), \(y = 8\), \(z = 2\), \(x' = - 4\) and \(y' = 7\) determine \(z'\) for the following equation. \[{x^4} + \frac{y}{z} = 2{x^2}{z^2} - 3\]
- n the following assume that \(x\), \(y\) and \(z\) are all functions of \(t\). Given \(x = - 2\), \(y = 3\), \(z = 4\), \(y' = 6\) and \(z' = 0\) determine \(x'\) for the following equation. \[x\,{y^2}{z^2} = {x^3} - {z^4} - 8y\]
- The sides of a square are increasing at a rate of 10 cm/sec. How fast is the area enclosed by the square increasing when the area is 150 cm2.
- The sides of an equilateral triangle are decreasing at a rate of 3 in/hr. How fast is the area enclosed by the triangle decreasing when the sides are 2 feet long?
- A spherical balloon is being filled in such a way that the surface area is increasing at a rate of 20 cm2/sec when the radius is 2 meters. At what rate is air being pumped in the balloon when the radius is 2 meters?
- A cylindrical tank of radius 2.5 feet is being drained of water at a rate of 0.25 ft3/sec. How fast is the height of the water decreasing?
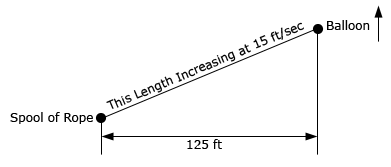
- A hot air balloon is attached to a spool of rope that is 125 feet away from the balloon when it is on the ground. The hot air balloon rises straight up in such a way that the length of rope increases at a rate of 15 ft/sec. How fast is the hot air balloon rising 20 seconds after it lifts off?
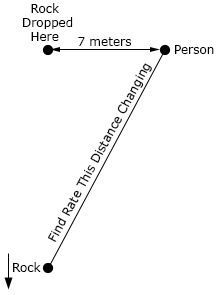
- A rock is dropped straight off a bridge that is 50 meters above the ground and falls at a speed of 10 m/sec. Another person is 7 meters away on the same bridge. At what rate is the distance between the rock and the second person increasing just as the rock hits the ground?
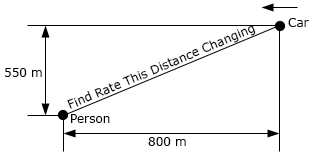
- A person is 550 meters away from a road and there is a car that is initially 800 meters away approaching the person at a speed of 45 m/sec. At what rate is the distance between the person and the car changing (a) 5 seconds after the start, (b) when the car is directly in front of the person and (c) 10 seconds after the car has passed the person.
- Two cars are initially 1200 miles apart. At the same time Car A starts driving at 35 mph to the east while Car B starts driving at 55 mph to the north (see sketch below for this initial setup). At what rate is the distance between the two cars changing after (a) 5 hours of travel, (b) 20 hours of travel and (c) 40 hours of travel?
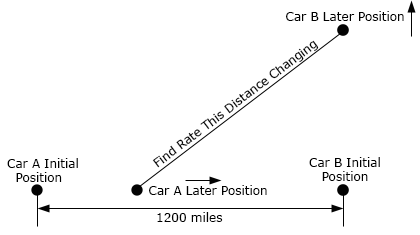
- 13. Repeat problem 12 above except for this problem assume that Car A starts traveling 4 hours after Car B starts traveling. For parts (a), (b) and (c) assume that these are travel times for Car B.
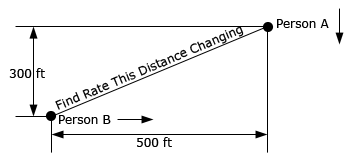
- Two people are on a city block. See the sketch below for placement and distances. Person A is on the northeast corner and Person B is on the southwest corner. Person A starts walking towards the southeast corner at a rate of 3 ft/sec. Four seconds later Person B starts walking towards the southeast corner at a rate of 2 ft/sec. At what rate is the distance between them changing (a) 10 seconds after Person A starts walking and (b) after Person A has covered half the distance?
- A person is standing 75 meters away from a kite and has a spool of string attached to the kite. The kite starts to rise straight up in the air at a rate of 2 m/sec and at the same time the person starts to move towards the kites launch point at a rate of 0.75 m/sec. Is the length string increasing or decreasing after (a) 4 seconds and (b) 20 seconds.
- A person lights the fuse on a model rocket and starts to move away from the rocket at a rate of 3 ft/sec. Five seconds after lighting the fuse the rocket launches straight up into the air at a rate of 10 ft/sec. Is the distance between the person and the rocket increasing or decreasing (a) 6 seconds after launch and (b) 12 seconds after launch?

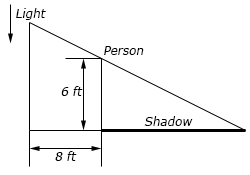
- A light is on a pole and is being lowered towards the ground at a rate of 9 in/sec. A 6 foot tall person is on the ground and 8 feet away from the pole. At what rate is the persons shadow increasing then the light is 15 feet above the ground?
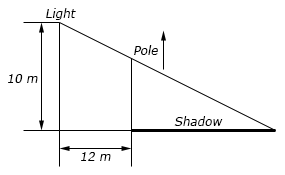
- A light is fixed on a wall 10 meters above the floor. Twelve meters away from the wall a pole is being raised straight up at a rate of 45 cm/sec. When the pole is 6 meters tall at what rate is the tip of the shadow moving (a) away from the pole and (b) away from the wall? Note the sketch below is not to scale…
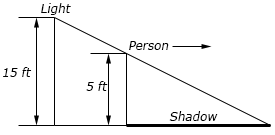
- A light is on the top of a 15 foot tall pole. A 5 foot tall person starts at the pole and moves away from the pole at a rate of 2.5 ft/sec. After moving for 8 seconds at what rate is the tip of the shadow moving (a) away from the person and (b) away from the pole?
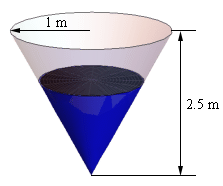
- A tank of water is in the shape of a cone (assume the “point” of the cone is pointing downwards) and is leaking water at a rate of 35 cm3/sec. The base radius of the tank is 1 meter and the height of the tank is 2.5 meters. When the depth of the water is 1.25 meters at what rate is the (a) depth changing and (b) the radius of the top of the water changing?
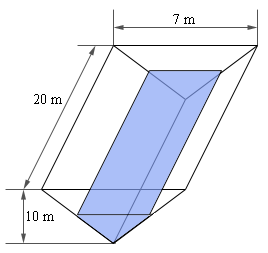
- A trough of water is 20 meters in length and its ends are in the shape of an isosceles triangle whose width is 7 meters and height is 10 meters. Assume that the two equal length sides of the triangle are the sides of the water tank and the other side of the triangle is the top of the tank and is parallel to the ground. Water is being pumped into the tank at a rate of 2 m3/min. When the water is 6 meters deep at what rate is (a) depth changing and (b) the width of the top of the water changing? Note the sketch below is not to scale…
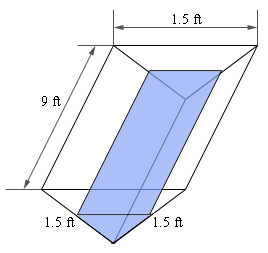
- A trough of water is 9 feet long and its ends are in the shape of an equilateral triangle whose sides are 1.5 feet long. Assume that the top of the tank is parallel to the ground. If water is being pumped out of the tank at a rate of 2 ft3/s at what rate is the depth of the water changing when the depth is 0.75 feet?
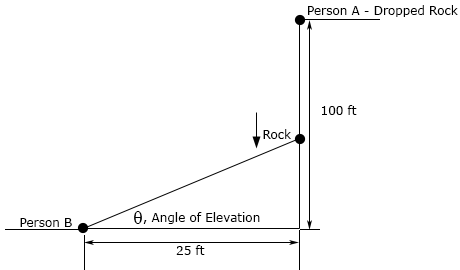
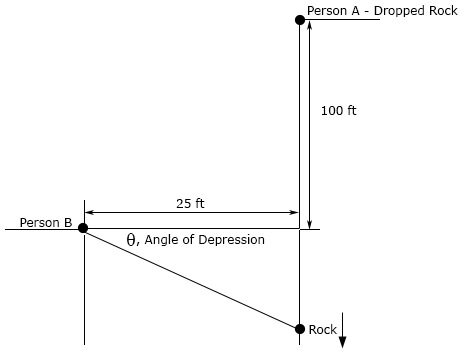
- The angle of elevation (depression) is the angle formed by a horizontal line and a line joining the observer’s eye to an object above (below) the horizontal line. Two people are on the roof of buildings separated by at 25 foot wide road. Person A is 100 feet above Person B and drops a rock off the roof of their building and it falls at a rate of 3 ft/sec. The sketches below are not to scale….
- At what rate is the angle of elevation changing as Person B watches the rock fall when the rock is 35 feet above Person B?
- At what rate is the angle of depression changing as Person B watches the rock fall when the rock is 65 feet below Person B?
- At what rate is the angle of elevation changing as Person B watches the rock fall when the rock is 35 feet above Person B?
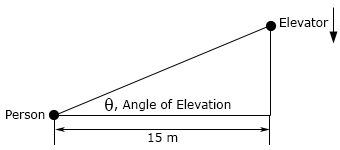
- The angle of elevation is the angle formed by a horizontal line and a line joining the observer’s eye to an object above the horizontal line. A person is standing 15 meters away from a building and watching an outside elevator move down the face of the building. When the angle of elevation is 1 radians it is changing at a rate of 0.15 radians/sec. At this point in time what is the speed of the elevator?
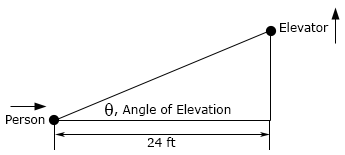
- The angle of elevation is the angle formed by a horizontal line and a line joining the observer’s eye to an object above the horizontal line. A person is 24 feet away from a building and watching an outside elevator move up the face of the building. The elevator is moving up at a rate of 4 ft/sec and the person is moving towards the building at a rate of 0.75 ft/sec. Assuming that the elevator started moving from the ground at the same time that the person started walking is the angle of elevation increasing or decreasing after 10 seconds?