Paul's Online Notes
Paul's Online Notes
Home / Calculus I / Applications of Derivatives / The Shape of a Graph, Part II
Show Mobile Notice Show All Notes Hide All Notes
Mobile Notice
You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.
Assignment Problems Notice
Please do not email me to get solutions and/or answers to these problems. I will not give them out under any circumstances nor will I respond to any requests to do so. The intent of these problems is for instructors to use them for assignments and having solutions/answers easily available defeats that purpose.

If you are looking for some problems with solutions you can find some by clicking on the "Practice Problems" link above.

Section 4.6 : The Shape of a Graph, Part II

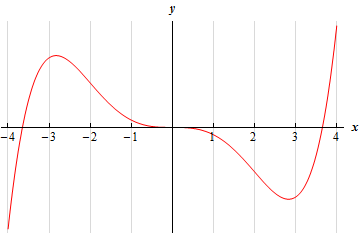
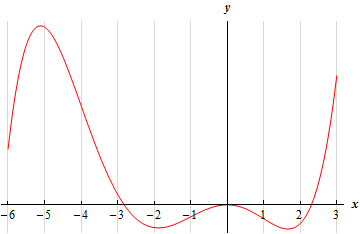
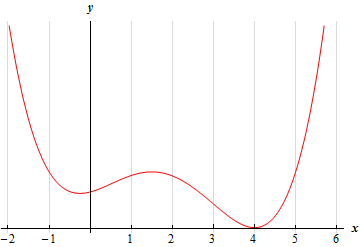
For problems 1 & 2 the graph of a function is given. Determine the intervals on which the function is concave up and concave down.

  1. This graph has no y scale. It starts in the third quadrant at x=-4 and increases to a peak at approximately x=-2.8 in the second quadrant and then starts to decrease and the graph is cupped downwards as it does this. At x=-2 the graph is still decreasing but now switches over to cupped vaguely upwards. This behavior continues until it reaches the origin where it is now decreasing with a vaguely cupped downward behavior. At x=2 the graph continues to decrease but switches over to being cupped upwards. The graph hits a valley at approximately x=2.8 in the fourth quadrant and then increases until it ends at x=4 in the first quadrant and the graph is still cupped upwards.
  2. This graph has no y scale. It starts in the second quadrant at x=-6 and increases to a peak at approximately x=-5.2 and then starts to decrease and the graph is cupped downwards as it does this. At x=-4 the graph is still decreasing but now switches over to cupped upwards. This behavior continues until it reaches a valley in the third quadrant at x=-2. At this point the graph now starts to increase and remains cupped upward. At x=-1 the graph is still increasing but switches over to being cupped downwards. The graph hits a peak at the origin and starts to decrease while still being cupped downward. At x=1 the graph is still decreasing but switches over to being cupped upwards. The graph hits a valley at approximately x=1.8 in the fourth quadrant and then starts to increase and continues to be cupped upward. This behavior continues until the graph ends at x=3 in the first quadrant.

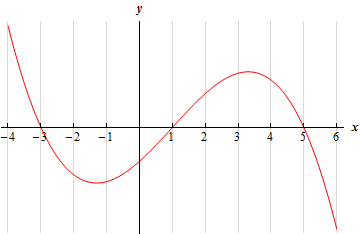
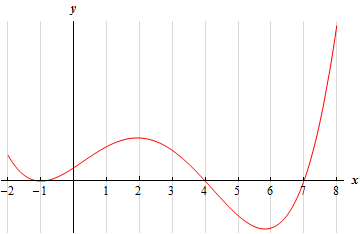
For problems 3 – 5 the graph of the 2nd derivative of a function is given. From this graph determine the intervals in which the function is concave up and concave down.

  1. This graph has no y scale. The graph starts at x=-4 in the second quadrant and goes down through the x-axis at x=-3 and hits a valley at approximately x=-1.5. It now goes up through the x-axis at x=1 and hits a peak at approximately x=3.2. It then goes back down through the x-axis at x=5 and ends at x=6 in the fourth quadrant.
  2. This graph has no y scale. The graph starts at x=-2 in the second quadrant and goes down and just touches the x-axis at x=-1 and then hits a peak at x=2. It now goes down through the x-axis at x=4 and hits a valley in the fourth quadrant at approximately x=5.8. It then goes back up through the x-axis at x=7 and ends at x=8 in the first quadrant.
  3. This graph has no y scale. The graph starts at x=-2 in the second quadrant and goes down to a peak, still in the second quadrant at approximately x=-0.5. It then goes up to a peak in the first quadrant at approximately x=1.5 and then goes down and just touches the x-axis at x=4. The graph then goes up to finish at around x=6 in the first quadrant.

For problems 6 – 18 answer each of the following.

  1. Determine the intervals on which the function is concave up and concave down.
  2. Determine the inflection points of the function.


  1. \(f\left( x \right) = {x^3} + 9{x^2} + 24x - 6\)
  2. \(Q\left( t \right) = {t^4} - 2{t^3} - 120{t^2} - 84t + 35\)
  3. \(h\left( z \right) = 3{z^5} - 20{z^4} + 40{z^3}\)
  4. \(g\left( w \right) = 5{w^4} - 2{w^3} - 18{w^2} + 108w - 12\)
  5. \(g\left( x \right) = 10 + 360x + 20{x^4} + 3{x^5} - {x^6}\)
  6. \(A\left( x \right) = 9x - 3{x^2} - 160\sin \left( {{\displaystyle \frac{x}{4}}} \right)\) on \(\left[ { - 20,11} \right]\)
  7. \(f\left( x \right) = 3\cos \left( {2x} \right) - {x^2} - 14\)on \(\left[ {0,6} \right]\)
  8. \(h\left( t \right) = 1 + 2{t^2} - \sin \left( {2t} \right)\) on \(\left[ { - 2,4} \right]\)
  9. \(R\left( v \right) = v{\left( {v - 8} \right)^{{\frac{1}{3}}}}\)
  10. \(g\left( x \right) = \left( {x - 1} \right){\left( {x + 3} \right)^{{\frac{2}{5}}}}\)
  11. \(f\left( x \right) = {{\bf{e}}^{4\,x}} - {{\bf{e}}^{ - \,x}}\)
  12. \(h\left( w \right) = {w^2}{{\bf{e}}^{ - w}}\)
  13. \(A\left( w \right) = {w^2} - \ln \left( {{w^2} + 1} \right)\)

For problems 19 – 33 answer each of the following.

  1. Identify the critical points of the function.
  2. Determine the intervals on which the function increases and decreases.
  3. Classify the critical points as relative maximums, relative minimums or neither.
  4. Determine the intervals on which the function is concave up and concave down.
  5. Determine the inflection points of the function.
  6. Use the information from steps (a) – (e) to sketch the graph of the function.

  1. \(f\left( x \right) = 10 - 30{x^2} + 2{x^3}\)
  2. \(G\left( t \right) = 14 + 4{t^3} - {t^4}\)
  3. \(h\left( w \right) = {w^4} + 4{w^3} - 18{w^2} - 9\)
  4. \(g\left( z \right) = 10{z^3} + 10{z^4} + 3{z^5}\)
  5. \(f\left( z \right) = {z^6} - 9{z^5} + 20{z^4} + 10\)
  6. \(Q\left( t \right) = 3t - 5\sin \left( {2t} \right)\) on \(\left[ { - 1,4} \right]\)
  7. \(g\left( x \right) = {\displaystyle \frac{1}{2}}x + \cos \left( {{\displaystyle \frac{1}{3}}x} \right)\) on \(\left[ { - 25,0} \right]\)
  8. \(h\left( x \right) = x{\left( {x - 4} \right)^{{\frac{1}{3}}}}\)
  9. \(f\left( t \right) = t\,\,\sqrt {{t^2} + 1} \)
  10. \(A\left( z \right) = {z^{{\frac{4}{5}}}}\,\left( {z - 27} \right)\)
  11. \(g\left( w \right) = {{\bf{e}}^{4\,w}} - {{\bf{e}}^{6\,w}}\)
  12. \(P\left( t \right) = 3t{{\bf{e}}^{1 - {\frac{1}{4}}{t^{\,2}}}}\)
  13. \(g\left( x \right) = {\left( {x + 1} \right)^3}{{\bf{e}}^{ - \,x}}\)
  14. \(h\left( z \right) = \ln \left( {{z^2} + z + 1} \right)\)
  15. \(f\left( w \right) = 2w - 8\ln \left( {{w^2} + 4} \right)\)
  16. Answer each of the following questions.
    1. What is the minimum degree of a polynomial that has exactly two inflection points.
    2. What is the minimum degree of a polynomial that has exactly three inflection points.
    3. What is the minimum degree of a polynomial that has exactly \(n\) inflection points.
  17. For some function, \(f\left( x \right)\), it is known that there is an inflection point at \(x = 3\). Answer each of the following questions about this function.
    1. What is the simplest form that the 2nd derivative of this function?
    2. Using your answer from (a) determine the most general form that the function itself can take.
    3. Given that \(f\left( 0 \right) = - 6\) and \(f\left( 3 \right) = 1\) find a function that will have an inflection point at \(x = 3\).

For problems 36 – 39 \(f\left( x \right)\) is a polynomial. Given the 2nd derivative of the function, classify, if possible, each of the given critical points as relative minimums or relative maximum. If it is not possible to classify the critical point(s) clearly explain why they cannot be classified.

  1. \(f''\left( x \right) = 3{x^2} - 4x - 15\). The critical points are : \(x = - 3\), \(x = 0\) and \(x = 5\).
  2. \(f''\left( x \right) = 4{x^3} - 21{x^2} - 24x + 68\). The critical points are : \(x = - 2\), \(x = 4\) and \(x = 7\).
  3. \(f''\left( x \right) = 23 + 18x - 9{x^2} - 4{x^3}\). The critical points are : \(x = - 4\), \(x = - 1\) and \(x = 3\).
  4. \(f''\left( x \right) = 216 - 410x + 249{x^2} - 60{x^3} + 5{x^4}\). The critical points are : \(x = 1\), \(x = 4\) and \(x = 5\).
  5. Use \(f\left( x \right) = {\left( {x + 1} \right)^3}{\left( {x - 1} \right)^4}\) for this problem.
    1. Determine the critical points for the function.
    2. Use the 2nd derivative test to classify the critical points as relative minimums or relative maximums. If it is not possible to classify the critical point(s) clearly explain why they cannot be classified.
    3. Use the 1st derivative test to classify the critical points as relative minimums, relative maximums or neither.
  6. Given that \(f\left( x \right)\) and \(g\left( x \right)\) are concave down functions. If we define \(h\left( x \right) = f\left( x \right) + g\left( x \right)\) show that \(h\left( x \right)\) is a concave down function.
  7. Given that \(f\left( x \right)\) is a concave up function. Determine a condition on \(g\left( x \right)\) for which \(h\left( x \right) = f\left( x \right) + g\left( x \right)\) will be a concave up function.
  8. For a function \(f\left( x \right)\) determine conditions on \(f\left( x \right)\) for which \(h\left( x \right) = {\left[ {f\left( x \right)} \right]^2}\) will be a concave up function. Note that there are several sets of conditions that can be used here. How many of them can you find?
[Contact Me] [Privacy Statement] [Site Help & FAQ] [Terms of Use]
© 2003 - 2024 Paul Dawkins
Page Last Modified : 11/16/2022