Section 3.3 : Circles
4. Determine the radius and center of the following circle and sketch the graph of the circle.
\[{x^2} + {\left( {y - 5} \right)^2} = 4\]Show All Steps Hide All Steps
Start SolutionThere really isn’t much to this problem. All we need to do is compare the equation we’ve been given to the standard form of the circle to determine the radius and center of the circle. For reference purposes here is the standard form of the circle.
\[{\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}\]First, notice that we can write the first term as,
\[{x^2} = {\left( {x - 0} \right)^2}\]and so we can now see that \(h = 0\)
Next, from the second term we can quickly see that \(k = 5\).
Finally, we see that \({r^2} = 4\) and so we must have \(r = 2\) .
Therefore, the radius of the circle is 2 and the center of the circle is \(\left( {0,5} \right)\) .
Show Step 2Here is a sketch of the circle.
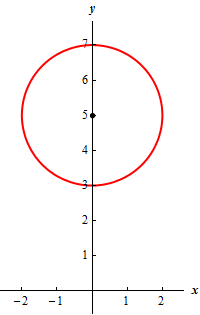
Remember that we can quickly graph the circle by starting at the center and then going right/left by the radius (2 for this problem) to get the right most/left most points. To get the top most/bottom most point all we need to do is start at the center and go up/down by the radius (again, 2 for this problem).