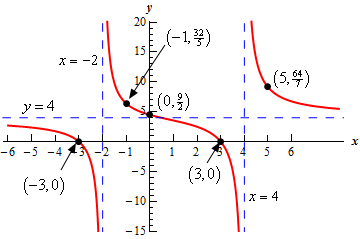Section 4.8 : Rational Functions
4. Sketch the graph of the following function. Clearly identify all intercepts and asymptotes.
\[f\left( x \right) = \frac{{4{x^2} - 36}}{{{x^2} - 2x - 8}}\]Show All Steps Hide All Steps
Start SolutionLet’s first find the intercepts for this function.
The \(y\)-intercept is the point \(\left( {0,f\left( 0 \right)} \right) = \left( {0,\frac{9}{2}} \right)\).
For the \(x\)-intercepts we set the numerator equal to zero and solve. Doing that for this problem gives,
\[4{x^2} - 36 = 0\hspace{0.25in} \to \hspace{0.25in}{x^2} = 9\hspace{0.25in} \to \hspace{0.25in}x = \pm 3\]So, the two \(x\)-intercepts for this problem are \(\left( { - 3,0} \right)\) and \(\left( {3,0} \right)\).
Show Step 2We can find any vertical asymptotes be setting the denominator equal to zero and solving. Doing that for this function gives,
\[{x^2} - 2x - 8 = \left( {x + 2} \right)\left( {x - 4} \right) = 0\hspace{0.25in} \to \hspace{0.25in}x = - 2,\,\,\,\,x = 4\]So, we’ll have two vertical asymptotes at \(x = - 2\) and \(x = 4\).
Show Step 3For this equation the largest exponent of \(x\) in both the numerator and denominator is 2. Therefore, the horizontal asymptote for this problem is then the coefficient of the \({x^2}\) in the numerator divided by the coefficient of the \({x^2}\) in the denominator. Or,
\[y = \frac{4}{1} = 4\] Show Step 4From Step 2 we saw we only have two vertical asymptotes and so we have three regions to our graph : \(x < - 2\), \( - 2 < x < 4\) and \(x > 4\).
We’ll need a point in each region to determine if it will be above or below the horizontal asymptote.
Also, as we discussed in the notes, there are a couple of possible different behaviors in the middle region. To determine just what the behavior is we need to get a couple of points in this region. The best idea for points in the middle region is check a couple of points close to the vertical asymptotes we know if the edge is going to be above or below the horizontal asymptote.
Here are some function evaluations for the points.
\[\begin{align*}f\left( { - 3} \right) & = 0 & \to \hspace{0.25in} & \left( { - 3,0} \right)\\ f\left( { - 1} \right) & = \frac{{32}}{5} & \to \hspace{0.25in} & \left( { - 1,\frac{{32}}{5}} \right)\\ f\left( 3 \right) & = 0 & \to \hspace{0.25in} & \left( {3,0} \right)\\ f\left( 5 \right) & = \frac{{64}}{7} & \to \hspace{0.25in} & \left( {5,\frac{{64}}{7}} \right)\end{align*}\]From the second and third points we see that the curve in the middle region should be below the horizontal asymptote at the right edge and above the horizontal asymptote at the left edge and so the curve will cross the horizontal asymptote in this region.
Also note that we used the two \(x\)-intercepts here because they worked out to be good choices for points to use.
Show Step 5Here is a sketch of the function with the points found above. The vertical and horizontal asymptotes are indicated with blue dashed lines.