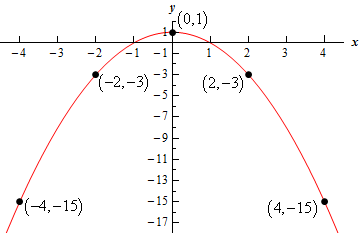Section 3.1 : Graphing
2. Construct a table of at least 4 ordered pairs of points on the graph of the following equation and use the ordered pairs from the table to sketch the graph of the equation.
\[y = 1 - {x^2}\]Show All Steps Hide All Steps
It is always a little difficult to know just what a good selection of values of \(x\) to use to determine the ordered pairs we will use to sketch the graph of an equation if you don’t know just what the graph looks like. Eventually you’ll do enough problems that you’ll start to develop some intuition on just what good values to try are for many equations.
For this equation a selection of points on either side of zero should be sufficient to get an idea of what the graph of this equation looks like. We’ll also include zero for no other reason that it will give an extra point on the graph.
Here is the table of points we’ll use for this problem.
| \(x\) | \(y\) | \(\left( {x,y} \right)\) |
|---|---|---|
| -4 | -15 | \(\left( { - 4, - 15} \right)\) |
| -2 | -3 | \(\left( { - 2, - 3} \right)\) |
| 0 | 1 | \(\left( {0,1} \right)\) |
| 2 | -3 | \(\left( {2, - 3} \right)\) |
| 4 | -15 | \(\left( {4, - 15} \right)\) |
We’ll leave the actual computations to you to verify but recall that all we do is take the \(x\) and plug it into the equation to determine the corresponding \(y\) value and then form the ordered pair for the \(x\) and its corresponding \(y\) value.
Show Step 2Here is a sketch of the equation.