Section 5.3 : Graphing Polynomials
3. Sketch the graph of each of the following polynomial.
\[h\left( x \right) = {x^4} + {x^3} - 12{x^2} + 4x + 16 = {\left( {x - 2} \right)^2}\left( {x + 1} \right)\left( {x + 4} \right)\]Show All Steps Hide All Steps
Start SolutionThe first step is to determine the zeroes of the polynomial and the multiplicity of each zero. For this problem the polynomial has already been factored.
We have the following list of zeroes and multiplicities.
\[\begin{align*}x & = - 4 :{\mbox{ multiplicity 1}}\\ x & = - 1 :{\mbox{ multiplicity 1}}\\ x & = 2\,\,:{\mbox{ multiplicity 2}}\end{align*}\]Because the multiplicity of \(x = - 4\) and \(x = - 1\) are odd we know that these point will correspond to \(x\)-intercepts that will cross the \(x\)-axis and \(x = 2\) has an even multiplicity and so we know that this point will correspond to an \(x\)-intercept that will just touch the \(x\)‑axis but not cross the \(x\)-axis.
Show Step 2The \(y\)-intercept for the function is : \(\left( {0,h\left( 0 \right)} \right) = \left( {0,16} \right)\).
Show Step 3The coefficient of the 4th degree term is positive and so we know that the polynomial will increase without bound at both ends.
Show Step 4Next, we need to pick a couple of points to graph. We’ll pick one point on the left and right end and it doesn’t matter which points to pick here so just pick one close to the zero on either end. We’ll also pick a point between each pair of zeroes and again it doesn’t really matter which points to pick so we’ll just pick points that are near the middle of each pair of zeroes.
Here are the function evaluations for this polynomial. We’ll leave it to you to verify the evaluations.
\[h\left( { - 5} \right) = 196\hspace{0.25in}h\left( { - 3} \right) = - 50\hspace{0.25in}h\left( 1 \right) = 10\hspace{0.25in}h\left( 3 \right) = 28\] Show Step 5Finally, here is a quick sketch of the polynomial.
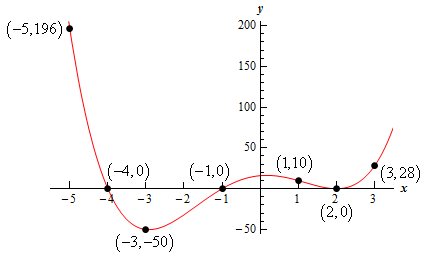
Note that your graph may not look quite like this one.
This is a computer generated graph and as such is very accurate. Using only Algebra techniques it can be quite difficult to approach this kind of accuracy. As long as the basic behavior of your graph is correct and you’ve got the extra points correctly graphed then you should have something that is close enough to the actual graph to work for a quick sketch.
For those interested, there are several techniques from a Calculus class that allow for a much more accurate sketch of the polynomial!