Section 4.4 : Hyperbolas
3. Sketch the graph of the following hyperbola.
\[3{\left( {x - 1} \right)^2} - \frac{{{{\left( {y + 1} \right)}^2}}}{2} = 1\]Show All Steps Hide All Steps
Start SolutionThe first step here is to simply compare our equation to the standard form of the hyperbola and identify all the important information. For reference purposes here is the standard form of the hyperbola that matches the one we have here.
\[\frac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} - \frac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1\]To help with the comparison let’s rewrite our equation a little to make it look more like the standard form.
\[\frac{{{{\left( {x - 1} \right)}^2}}}{{\frac{1}{3}}} - \frac{{{{\left( {y + 1} \right)}^2}}}{2} = 1\]In order to properly identify \(a\) and \(b\) the numbers need to be in the denominator. So, we needed to move the 3 from the numerator of the first term into a 1/3 in the denominator.
Comparing our equation to this we can see we have the following information.
\[h = 1\hspace{0.25in}k = - 1\hspace{0.25in}a = \sqrt {\frac{1}{3}} = \frac{1}{{\sqrt 3 }}\hspace{0.25in}b = \sqrt 2 \]Do not get excited about the square roots in the \(a\) and \(b\). They will be present on occasion and so we need to be able to deal with them. Also, in order to make it slightly easier to deal with we did simplfy the \(a\) by taking the square root of both the numerator (which was really easy to compute) and the denominator.
Because the \(x\) term is the positive term we know that this hyperbola will open right and left.
Show Step 2With the information we found in the first step we can see that the center of the hyperbola is \(\left( {1, - 1} \right)\).
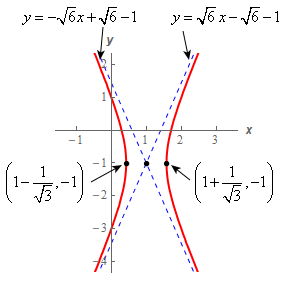
The vertices of hyperbola are : \(\left( {1 - \frac{1}{{\sqrt 3 }}, - 1} \right) = \left( {0.4226, - 1} \right)\) and \(\left( {1 + \frac{1}{{\sqrt 3 }}, - 1} \right) = \left( {1.5774, - 1} \right)\).
The equations of the two asymptotes are,
\[y = - 1 + \frac{{\sqrt 2 }}{{{}^{1}/{}_{{\sqrt 3 }}}}\left( {x - 1} \right) = \sqrt 6 \,x - \sqrt 6 - 1\hspace{0.25in}y = - 1 - \frac{{\sqrt 2 }}{{{}^{1}/{}_{{\sqrt 3 }}}}\left( {x - 1} \right) = - \sqrt 6 \,x + \sqrt 6 - 1\]The asymptotes in this case are somewhat messier than we are used to dealing with because of the square roots but they work the same way all lines do. The only difference is the numbers are simply messier.
Also note that we simplified the slopes as follows,
\[\frac{{\sqrt 2 }}{{{}^{1}/{}_{{\sqrt 3 }}}} = \sqrt 2 \,\,\frac{{\sqrt 3 }}{1} = \sqrt {2\left( 3 \right)} = \sqrt 6 \] Show Step 3Here is a sketch of the hyperbola including the points and asymptotes we found above.