For this problem all we need to do is recall the Transformations section from a couple of chapters ago. Using the “base” function of \(f\left( x \right) = \ln \left( x \right)\) the function for this part can be written as,

Therefore, the graph for this part is just the graph of \(f\left( x \right)\) shifted left by 5.

The graph of this function is shown below. The blue dashed line is the “base” function, \(f\left( x \right)\), and the red solid line is the graph for this part, \(g\left( x \right)\).

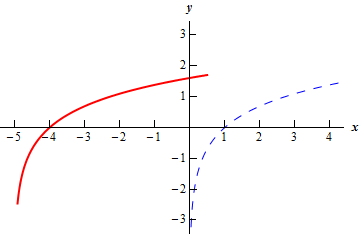
Do not get excited about the fact that we plugged negative values of \(x\) into the function! The problem with negative values is not the values we plug into a logarithm. Instead the problem with negative values is when we go to evaluate the logarithm.

It is perfectly fine to plug negative values into a logarithm as long as we don’t end up actually evaluating a negative number. So, in this case we can see that as long as we require \(x > - 5\) then \(x + 5 > 0\) and so those are acceptable values of \(x\) to plug in since we aren’t going to evaluate negative number in the logarithm.

Note however that we do have avoid \(x < - 5\) since that would mean evaluating logarithms at negative numbers.