Algebra - Parabolas

Hide Mobile Notice

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 4.2 : Parabolas

Back to Problem List

5. Sketch the graph of the following parabola. The graph should contain the vertex, the $y$ ‑intercept, $x$ -intercepts (if any) and at least one point on either side of the vertex.

$f\left( x \right) = 2{x^2} - 12x + 26$

Show All Steps Hide All Steps

Start Solution

Let’s find the vertex first. In this case the equation is in the form $f\left( x \right) = a{x^2} + bx + c$ . And so we know the vertex is the point $\left( { - \frac{b}{{2a}},f\left( { - \frac{b}{{2a}}} \right)} \right)$ . The vertex is then,

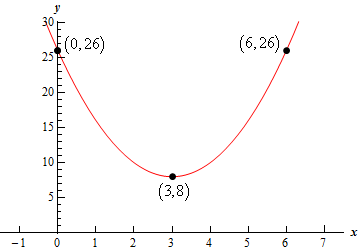
$\left( { - \frac{{ - 12}}{{2\left( 2 \right)}},f\left( { - \frac{{ - 12}}{{2\left( 2 \right)}}} \right)} \right) = \left( {3,f\left( 3 \right)} \right) = \left( {3,8} \right)$

Also note that $a = 2 > 0$ for this parabola and so the parabola will open upwards.

Show Step 2

The $y$ -intercept is just the point $\left( {0,f\left( 0 \right)} \right)$ . A quick function evaluation gives us that $f\left( 0 \right) = 26$ and so for our equation the $y$ -intercept is $\left( {0,26} \right)$ .

Show Step 3

For the $x$ -intercepts we just need to solve the equation $f\left( x \right) = 0$ . So, let’s solve that for our equation.

$2{x^2} - 12x + 26 = 0\,\,\,\,\, \to \,\,\,\,\,\,x = \frac{{12 \pm \sqrt {{{\left( { - 12} \right)}^2} - 4\left( 2 \right)\left( {26} \right)} }}{{2\left( 2 \right)}} = \frac{{12 \pm \sqrt { - 64} }}{4} = 3 \pm 2i$

So, in this case the solutions to this equation are complex numbers and so we know that this parabola will have no $x$ -intercepts.

Note that we did not really need to solve the equation above to see that there would be no $x$ -intercepts for this problem. An alternate method would be to do the following analysis.

From the first step we found that the vertex was $\left( {3,8} \right)$ , which is above the $x$ -axis, and we also noted that the parabola opened upwards. So, the parabola starts above the $x$ -axis and opens upwards and we know that once a parabola starts opening in a given direction it won’t turn around and start going in the opposite direction. Therefore, because there is no way for the parabola to go down to the $x$ -axis, there is no way for there to be $x$ ‑intercepts for this problem.

Show Step 4

In this case all we have are the vertex and the $y$ -intercept (which is on the left side of the vertex). So, we’ll need a point that is on the right side of the vertex and we can find the point on the left side of the vertex that corresponds to the $y$ -intercept for this point.

The $y$ -intercept is a distance of 3 to the left of the vertex and so there will be a corresponding point at the same $y$ value to the right and it will be a distance of 3 to the right of the vertex. Therefore, the point to the right of the vertex corresponding to the y‑intercept is $\left( {6,26} \right)$ .

Show Step 5

Here is a sketch of the parabola including all the points we found above.