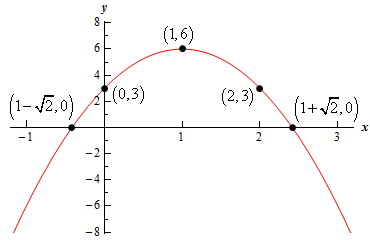
Section 4.2 : Parabolas
7. Sketch the graph of the following parabola. The graph should contain the vertex, the \(y\)‑intercept, \(x\)-intercepts (if any) and at least one point on either side of the vertex.
\[f\left( x \right) = - 3{x^2} + 6x + 3\]Show All Steps Hide All Steps
Start SolutionLet’s find the vertex first. In this case the equation is in the form \(f\left( x \right) = a{x^2} + bx + c\). And so we know the vertex is the point \(\left( { - \frac{b}{{2a}},f\left( { - \frac{b}{{2a}}} \right)} \right)\). The vertex is then,
\[\left( { - \frac{6}{{2\left( { - 3} \right)}},f\left( { - \frac{6}{{2\left( { - 3} \right)}}} \right)} \right) = \left( {1,f\left( 1 \right)} \right) = \left( {1,6} \right)\]Also note that \(a = - 3 < 0\) for this parabola and so the parabola will open downwards.
Show Step 2The \(y\)-intercept is just the point \(\left( {0,f\left( 0 \right)} \right)\). A quick function evaluation gives us that \(f\left( 0 \right) = 3\) and so for our equation the \(y\)-intercept is \(\left( {0,3} \right)\).
Show Step 3For the \(x\)-intercepts we just need to solve the equation \(f\left( x \right) = 0\). So, let’s solve that for our equation.
\[ - 3{x^2} + 6x + 3 = 0\hspace{0.25in} \to \hspace{0.25in} x = \frac{{ - 6 \pm \sqrt {{6^2} - 4\left( { - 3} \right)\left( 3 \right)} }}{{2\left( { - 3} \right)}} = \frac{{ - 6 \pm \sqrt {72} }}{{ - 6}} = \frac{{ - 6 \pm 6\sqrt 2 }}{{ - 6}} = 1 \pm \sqrt 2 \]The two \(x\)-intercepts for this parabola are then : \(\left( {1 - \sqrt 2 ,0} \right) = \left( { - 0.4142,0} \right)\) and \(\left( {1 + \sqrt 2 ,0} \right) = \left( {2.4142,0} \right)\).
Show Step 4Because we had two \(x\)-intercepts for this parabola we already have at least one point on either side of the vertex and so we don’t really need to find any more points for our graph.
However, just for the practice let’s find the point corresponding to the \(y\)-intercept on the other side the vertex.
The \(y\)-intercept is a distance of 1 to the left of the vertex and so there will be a corresponding point at the same \(y\) value to the right and it will be a distance of 1 to the right of the vertex. Therefore, the point to the right of the vertex corresponding to the y‑intercept is \(\left( {2,3} \right)\).
Show Step 5Here is a sketch of the parabola including all the points we found above.