Section 2.13 : Rational Inequalities
5. Solve the following inequality.
\[u \le \frac{4}{{u - 3}}\]Show All Steps Hide All Steps
Start SolutionThe first thing we need to do is get a zero on one side of the inequality and then, if possible, factor the numerator and denominator as much as possible.
So, we first need to get zero on one side of the inequality. \[u - \frac{4}{{u - 3}} \le 0\]We now need to combine the two terms in to a single rational expression.
\[\begin{align*}\frac{{u\left( {u - 3} \right)}}{{u - 3}} - \frac{4}{{u - 3}} & \le 0\\ \frac{{{u^2} - 3u - 4}}{{u - 3}} & \le 0\end{align*}\]Finally, we need to factor the numerator.
\[\frac{{\left( {u - 4} \right)\left( {u + 1} \right)}}{{u - 3}} \le 0\]Recall from the discussion in the notes for this section that the rational expression can only change sign where the numerator is zero and/or where the denominator is zero.
We can see that the numerator will be zero at,
\[u = - 1\hspace{0.25in}\hspace{0.25in}u = 4\]and the denominator will be zero at,
\[u = 3\]Just as we did with polynomial inequalities all we need to do is check the rational expression at test points in each region between the points from the previous step. The rational expression will have the same sign as the sign at the test point since it can only change sign at those points.
Here is a sketch of a number line with the points from the previous step graphed on it. We’ll also show the test point computations on the number line as well. Here is the number line.
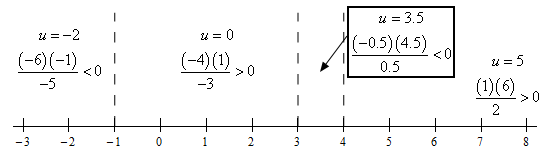
All we need to do now is get the solution from the number line in the previous step. Here is both the inequality and interval notation from of the answer.
\[\require{bbox} \bbox[2pt,border:1px solid black]{\begin{array}{c} u \le - 1\hspace{0.25in}{\mbox{and }}\hspace{0.25in} 3 < u \le 4\\ \left( { - \infty , - 1} \right] \hspace{0.25in} {\mbox{and }}\hspace{0.25in} \left( {3,4} \right]\end{array}}\]Be careful with the endpoints for this problem. Because we have an equal sign in the original inequality we need to include \(u = - 1\) and \(u = 4\) because the numerator and hence the rational expression will be zero there. However, we can’t include \(u = 3\) because the denominator is zero there and so the rational expression has division by zero at that point!