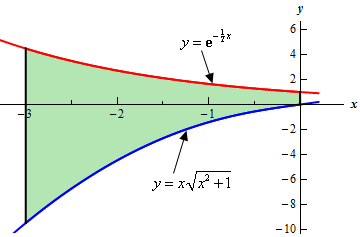
It should be clear from the graph that the upper function is \(y = {{\bf{e}}^{ - \,\,\frac{1}{2}x}}\) and the lower function is \(y = x\sqrt {{x^2} + 1} \).

Next, we were given limits on \(x\) in the problem statement (recall that the \(y\)-axis is just the line \(x = 0\)!) and we can see that the two curves do not intersect in that range. Note that this is something that we can’t always guarantee and so we need the graph to verify if the curves intersect or not. We should never just assume that because limits on \(x\) were given in the problem statement that the curves will not intersect anywhere between the given limits.

So, because the curves do not intersect we will be able to find the area with a single integral using the limits : \( - 3 \le x \le 0\).

Show Step 3

At this point there isn’t much to do other than step up the integral and evaluate it.

We are assuming that you are comfortable with basic integration techniques, including substitution since that will be needed here, so we’ll not be including any discussion of the actual integration process here and we will be skipping some of the intermediate steps.

The area is,

\[A = \int_{{ - 3}}^{0}{{{{\bf{e}}^{ - \,\,\frac{1}{2}x}} - x\sqrt {{x^2} + 1} \,dx}} = \left. {\left( { - 2{{\bf{e}}^{ - \,\,\frac{1}{2}x}} - \frac{1}{3}{{\left( {{x^2} + 1} \right)}^{\frac{3}{2}}}} \right)} \right|_{ - 3}^0 = \require{bbox} \bbox[2pt,border:1px solid black]{{ - \frac{7}{3} + 2{{\bf{e}}^{\frac{3}{2}}} + \frac{1}{3}{{10}^{\frac{3}{2}}} = 17.17097}}\]