Calculus I - Minimum and Maximum Values

Show Mobile Notice Show All Notes Hide All Notes

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best views in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (should be able to scroll to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 4.3 : Minimum and Maximum Values

Back to Problem List

1. Below is the graph of some function, \(f\left( x \right)\). Identify all of the relative extrema and absolute extrema of the function.

Show Solution

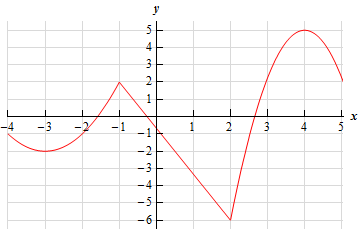
There really isn’t all that much to this problem. We know that absolute extrema are the highest/lowest point on the graph and that they may occur at the endpoints or in the interior of the graph. Relative extrema on the other hand, are “humps” or “bumps” in the graph where in the region around that point the “bump” is a maximum or minimum. Also recall that relative extrema only occur in the interior of the graph and not at the end points of the interval.

Also recall that relative extrema can also be absolute extrema.

So, we have the following absolute/relative extrema.

Absolute Maximum : \(\left( {4,5} \right)\)

Absolute Minimum : \(\left( {2, - 6} \right)\)

Relative Maximums : \(\left( { - 1,2} \right)\) and \(\left( {4,5} \right)\)

Relative Minimums : \(\left( { - 3, - 2} \right)\) and \(\left( {2, - 6} \right)\)