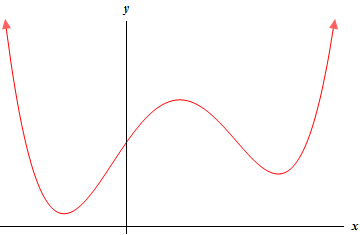
So, we need a graph of some function (not the function itself, only the graph) that meets the given conditions. We were not given an interval as one of the conditions so it’s okay to assume that the interval is \(\left( { - \infty ,\infty } \right)\) for this problem.

From the first condition we know that we can’t have any holes or breaks in the graph in order for the function to be continuous.

Now let’s take care of the next two conditions as they are related to each other. By this point we’ve seen enough sketches of graphs to have a pretty good idea of what absolute and relative minimums looks like. So, we’re going to need two downwards pointing “bumps” in the graph to give use the two relative minimums. Also, one of them must be the lowest point on the graph and other must be higher so it is not also an absolute minimum.

Next, we want to think about how to connect the two relative minimums. This is also where the fourth condition comes in. As we’ll see because we have a continuous function we’ll need that to connect the two relative minimums.

Let’s start with the leftmost relative minimum. In order for it to be a minimum the graph must be increasing as we move to the right. However, if we also want to get the minimum to the right of this the graph will have to, at some point, start decreasing again. If you think about it that is exactly what a relative maximum will look like. So, in moving from the leftmost relative minimum to the rightmost relative minimum we must have a relative maximum between them and so the fourth condition is automatically met.

Note that if we don’t insist on a continuous function it is possible to get from one to the other without having a relative maximum. All it would take is to have a division by zero discontinuity somewhere between the two relative minimums in which the graph goes to positive infinity on both sides of the discontinuity.

This would maintain the relative minimums and at the same time would not be a relative maximum.

Now let’s deal with the final condition. In order for the graph to have no absolute maximum all we really need to do is make sure that the graph increases without bound as we move to the right and left of the graph. This will also match up nicely with the relative minimums that we are required to have.

To the left of the leftmost relative minimum the graph must be increasing and so we may as well just let it increase forever on that side. Likewise, on the right side of the rightmost relative minimum the graph will need to be increasing. So, again let’s just let the graph increase forever on that side.

There are literally an infinite number of graphs that we could do here. Some will be more complicated that others, but here is probably one of the simpler graphs that we could use here.