Section 4.9 : More Optimization
4. An 80 cm piece of wire is cut into two pieces. One piece is bent into an equilateral triangle and the other will be bent into a rectangle with one side 4 times the length of the other side. Determine where, if anywhere, the wire should be cut to maximize the area enclosed by the two figures.
Show All Steps Hide All Steps
Start SolutionBefore we do a sketch we’ll need to do a little setup. Let’s suppose that the length of the piece of wire that goes to the rectangle is \(x\). This means that the length of the piece of wire going to the triangle is \(80 - x\).
We know that the length of each side of the triangle are equal and so must have length \({\frac{1}{3}}\left( {80 - x} \right)\). We also know that the interior angles of the triangle are \({\frac{\pi}{3}}\) and so the height of the triangle is \({\frac{1}{3}}\left( {80 - x} \right)\sin \left( {{\frac{\pi}{3}}} \right) = \frac{\sqrt{3}}{6} \left( {80 - x} \right)\).
For the rectangle let’s suppose that the length of the smaller side is \(L\) and so the length of the larger side is 4\(L\). Next, we know that the total perimeter of the rectangle is \(x\) and so we must have,
\[x = 2\left( L \right) + 2\left( {4L} \right) = 10L\hspace{0.5in} \to \hspace{0.5in}L = \frac{x}{10} \]Now that we have all the various lengths of the figures in terms of \(x\) (which will make the work here a little easier) let’s summarize everything up with the following figure.
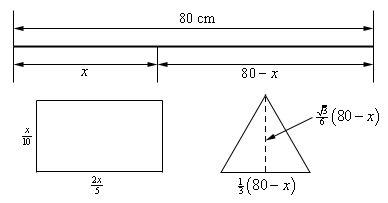
Next, we need to set up the constraint and equation that we are being asked to optimize.
This is one of those cases where we really don’t have a constraint equation to work with. The constraint is the length of the wire (80 cm), but we took that into account when we set up our figure above so there isn’t anything to do with that in this case.
We are being asked to maximize the enclosed area of the two figures and so here is the total area of the enclosed figures.
\[A\left( x \right) = \left( \frac{x}{10} \right)\left( \frac{2x}{5} \right) + {\frac{1}{2}}\left[ {{\frac{1}{3}}\left( {80 - x} \right)} \right]\left[ \frac{\sqrt{3}}{6} {\left( {80 - x} \right)} \right] = \frac{x^{2}}{25} + \frac{\sqrt{3}}{36} {\left( {80 - x} \right)^2}\] Show Step 3Finding the critical point(s) for this shouldn’t be too difficult at this point (although the Algebra will be a little messy). Here is the derivative.
\[A'\left( x \right) = \frac{2x}{25} - \frac{\sqrt{3}}{18} \left( {80 - x} \right)\]From this it looks like we get a single critical point,
\[x=\frac{\frac{40\sqrt{3}}{9}}{\frac{2}{25}+\frac{\sqrt{3}}{18}}=43.6828\] Show Step 4The second derivative of the area function is,
\[A''\left( x \right) = \frac{2}{25} + \frac{\sqrt{3}}{18} \]From this we can see that the second derivative is always positive. Therefore \(A\left( x \right)\) will always be concave up and so the single critical point we got in Step 4 must be a relative minimum and hence must be the value of \(x\) (i.e. the cut point) that will give the minimum enclosed area.
This is a problem however as we were asked for the maximum enclosed area. This is the reason for this step being in every problem that we’ve worked over the last couple of sections. Far too often students get to this point, get a single answer and then just assume that it must be the correct answer and don’t bother doing any kind of checking to verify if it is the correct answer.
After all there was a single value so there is no choice for it to be correct. Right? Well, no. As we’ll seen here it in fact is not the correct answer.
Show Step 5So, what to do? We’ll recall for the problem statement that we were asked to,
“Determine where, if anywhere, the wire should be cut to maximize the area enclosed by the two figures.”
The “if anywhere” portion seems to suggest that we may not want to cut it at all. Maybe all of the wire should go to the rectangle (corresponding to \(x = 80\) above) or maybe all of the wire should to the triangle (corresponding to \(x = 0\) above).
So, all we need to do is plug \(x = 80\) and \(x = 0\) into the area function and determine which will give the largest area.
\[\begin{align*}A\left( 0 \right) &= 307.92 & \hspace{0.75in} & {\mbox{All wire goes to triangle.}}\\ A\left( {43.6828} \right) & = 139.785&\hspace{0.75in} & {\mbox{Wire goes to both triangle and rectangle.}}\\ A\left( {80} \right) & = 256 & \hspace{0.75in} & {\mbox{All wire goes to rectangle}}\end{align*}\]Note that we included the critical point above just to make it really clear that it will not in fact give the maximum area. We didn’t really need to include it here as we already knew it wouldn’t work for us.
From the function evaluations above it looks like we’ll need to take all of the wire and bend it into an equilateral triangle in order to get the maximum area.