Section 4.9 : More Optimization
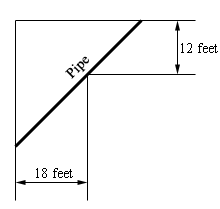
6. A piece of pipe is being carried down a hallway that is 18 feet wide. At the end of the hallway there is a right-angled turn and the hallway narrows down to 12 feet wide. What is the longest pipe (always keeping it horizontal) that can be carried around the turn in the hallway?
Show All Steps Hide All Steps
Start SolutionLet’s start with a quick sketch of the pipe and hallways with all the important quantities given.
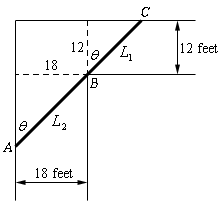
Next, we need to set up the constraint and equation that we are being asked to optimize.
As we discussed in the similar problem in the notes for this section we actually need to minimize the total length of the pipe. The equation we need to minimize is then,
\[L = {L_1} + {L_2}\]Also as we discussed in the notes problem with actually have two constraints : the widths of the two hallways. We can easily solve for these in terms of the angle \(\theta \).
\[{L_1} = 12\sec \theta \hspace{0.5in}{L_2} = 18\csc \theta \]As discussed in the notes problem we also know that we must have \(0 < \theta < {\frac{\pi}{2}}\).
Show Step 3All we need to do here is plug our two constraints in the length function to get a function in terms of \(\theta \) that we can minimize.
\[L\left( \theta \right) = 12\sec \theta + 18\csc \theta \] Show Step 4The derivative of the length function is,
\[L'\left( \theta \right) = 12\sec \theta \tan \theta - 18\csc \theta \cot \theta \]Next, we need to set this equal to zero and solve this for \(\theta \) to get the critical point that is in the range \(0 < \theta < {\frac{\pi}{2}}\).
\[\begin{align*}12\sec \theta \tan \theta & = 18\csc \theta \cot \theta \\ \frac{{\sec \theta \tan \theta }}{{\csc \theta \cot \theta }} & = \frac{{18}}{{12}}\\ {\tan ^3}\theta & = \frac{3}{2}\end{align*}\]The critical point that we need is then : \(\theta = {\tan ^{ - 1}}\left( {\sqrt[3]{{{\frac{3}{2}}}}} \right) = 0.8528\).
Show Step 5Verifying that this is the value that gives the minimum is a little trickier than the other problems.
As noted in the notes for this section as we move \(\theta \to 0\) we have \(L \to \infty \) and as we move \(\theta \to {\frac{\pi}{2}}\) we have \(L \to \infty \). Therefore, on either side of \(\theta = 0.8528\) radians the length of the pipe is increasing to infinity as we move towards the end of the range.
Therefore, this angle must give us the minimum length of the pipe and so is the largest pipe that we can fit around corner.
Show Step 6The largest pipe that we can fit around the corner is then,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{L\left( {0.8528} \right) = 42.1409{\mbox{ feet}}}}\]