Section 6.4 : Volume With Cylinders
6. Use the method of cylinders to determine the volume of the solid obtained by rotating the region bounded by \(x = {y^2} - 4\) and \(x = 6 - 3y\) about the line \(y = - 8\).
Show All Steps Hide All Steps
We need to start the problem somewhere so let’s start “simple”.
Knowing what the bounded region looks like will definitely help for most of these types of problems since we need to know how all the curves relate to each other when we go to set up the area formula and we’ll need limits for the integral which the graph will often help with.
Here is a sketch of the bounded region with the axis of rotation shown.
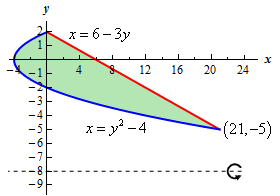
To get the intersection points shown above, which we’ll need in a bit, all we need to do is set the two equations equal and solve.
\[\begin{align*}{y^2} - 4 & = 6 - 3y\\ {y^2} + 3y - 10 & = 0\\ \left( {y + 5} \right)\left( {y - 2} \right) & = 0\hspace{0.25in} \Rightarrow \hspace{0.25in} y = - 5,\,\,\,y = 2 \hspace{0.25in} \Rightarrow \hspace{0.25in}\left( { 21, - 5} \right)\,\,\,\,\& \,\,\,\,\left( {0, 2} \right)\end{align*}\]Hint : Give a good attempt at sketching what the solid of revolution looks like and sketch in a representative cylinder.
Note that this can be a difficult thing to do especially if you aren’t a very visual person. However, having a representative cylinder can be of great help when we go to write down the area formula. Also, getting the representative cylinder can be difficult without a sketch of the solid of revolution. So, do the best you can at getting these sketches.
Note that this can be a difficult thing to do especially if you aren’t a very visual person. However, having a representative cylinder can be of great help when we go to write down the area formula. Also, getting the representative cylinder can be difficult without a sketch of the solid of revolution. So, do the best you can at getting these sketches.
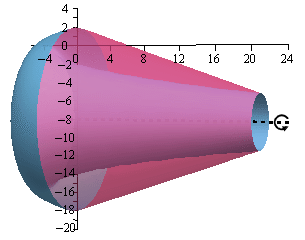
Here is a sketch of the solid of revolution.
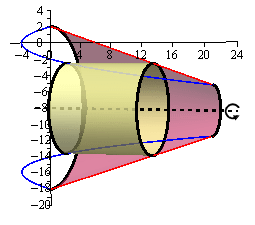
Here are a couple of sketches of a representative cylinder. The image on the left shows a representative cylinder with the front half of the solid cut away and the image on the right shows a representative cylinder with a “wire frame” of the back half of the solid (i.e. the curves representing the edges of the of the back half of the solid).
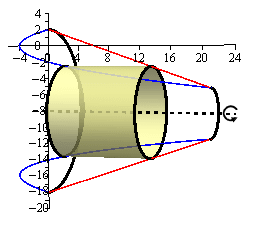
We now need to find a formula for the surface area of the cylinder. Because we are using cylinders that are centered on a horizontal axis (i.e. parallel to the \(x\)-axis) we know that the area formula will need to be in terms of \(y\). Therefore, the equations of the curves will need to be in terms of \(y\) (which in this case they already are).
Here is another sketch of a representative cylinder with all of the various quantities we need put into it.
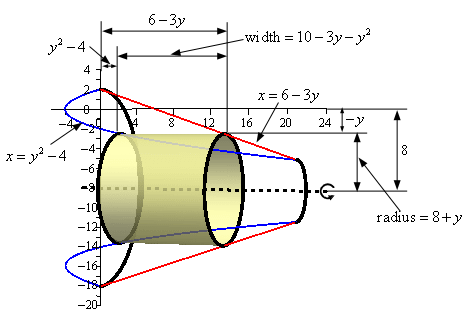
From the sketch we can see the cylinder is centered on the line \(y = - 8\) and the upper edge of the cylinder is at some \(y\).
The radius of the cylinder is a little tricky for this problem.
First, notice that the axis of rotation is a distance of 8 below the \(x\)-axis. Next, the upper edge of the cylinder is at some \(y\) however because \(y\) is negative at the point where we drew the cylinder that means that the distance of the upper edge below the \(x\)-axis is in fact \( - y\). The minus is needed to turn this into a positive quantity that we need for distance. The radius for this cylinder is then the difference of these two distances or,
\[8 - \left( { - y} \right) = 8 + y\]Now, note that when the upper edge of the cylinder rises above the \(x\)-axis the distance of the upper edge above the \(x\)-axis will be just \(y\). This time because \(y\) is positive we don’t need the minus sign (and in fact don’t want it because that would turn the distance into a negative quantity). The radius is then the distance of the axis of rotation from the \(x\)-axis (still a distance of 8) plus by the distance of the upper edge above the \(x\)-axis (which is \(y\)) or,
\[8 + y\]In either case we get the same radius.
The right edge of the cylinder is on the curve defining the right portion of the solid and is a distance of \(6 - 3y\) from the \(y\)-axis. The left edge of the cylinder is on the curve defining the left portion of the solid and is a distance of \({y^2} - 4\) from the \(y\)-axis. The width then is the difference of these two.
So, the radius and width of the cylinder are,
\[{\mbox{Radius}} = 8 + y\hspace{0.25in}\hspace{0.25in}{\mbox{Width}} = 6 - 3y - \left( {{y^2} - 4} \right) = 10 - 3y - {y^2}\]The area of the cylinder is then,
\[A\left( y \right) = 2\pi \left( {{\mbox{Radius}}} \right)\left( {{\mbox{Height}}} \right) = 2\pi \left( {8 + y} \right)\left( {10 - 3y - {y^2}} \right) = 2\pi \left( {80 - 14y - 11{y^2} - {y^3}} \right)\] Show Step 4The final step is to then set up the integral for the volume and evaluate it.
From the graph from Step 1 we can see that the “first” cylinder in the solid would occur at \(y = - 5\) and the “last” cylinder would occur at \(y = 2\). Our limits are then : \( - 5 \le y \le 2\).
The volume is then,
\[V = \int_{{ - 5}}^{2}{{2\pi \left( {80 - 14y - 11{y^2} - {y^3}} \right)\,dy}} = 2\left. {\pi \left( {80y - 7{y^2} - \frac{{11}}{3}{y^3} - \frac{1}{4}{y^4}} \right)} \right|_{ - 5}^2 = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{4459}}{6}\pi }}\]