Section 7.10 : Approximating Definite Integrals
2. Using \(n = 6\) approximate the value of \(\displaystyle \int_{{ - 1}}^{2}{{\sqrt {{{\bf{e}}^{ - \,{x^{\,2}}}} + 1} \,dx}}\) using
- the Midpoint Rule,
- the Trapezoid Rule, and
- Simpson’s Rule.
Use at least 6 decimal places of accuracy for your work.
Show All Solutions Hide All Solutions a Midpoint Rule Show SolutionWhile it’s not really needed to do the problem here is a sketch of the graph.
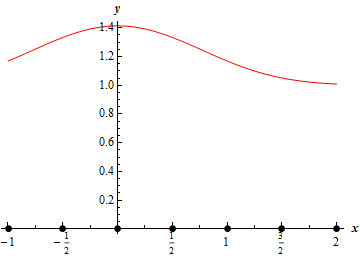
We know that we need to divide the interval \(\left[ { - 1,2} \right]\) into 6 subintervals each with width,
\[\Delta x = \frac{{2 - \left( { - 1} \right)}}{6} = \frac{1}{2}\]The endpoints of each of these subintervals are represented by the dots on the \(x\) axis on the graph above.
The tick marks between each dot represents the midpoint of each of the subintervals. The \(x\)-values of the midpoints for each of the subintervals are then,
\[ - \frac{3}{4},\hspace{0.25in} - \frac{1}{4},\hspace{0.25in}\frac{1}{4},\hspace{0.25in}\frac{3}{4},\hspace{0.25in}\frac{5}{4},\hspace{0.25in}\frac{7}{4}\]So, to use the Midpoint Rule to approximate the value of the integral all we need to do is plug into the formula. Doing this gives,
\[\begin{align*}\int_{{ - 1}}^{2}{{\sqrt {{{\bf{e}}^{ - \,{x^{\,2}}}} + 1} \,dx}} & \approx \left( {\frac{1}{2}} \right)\left[ {f\left( { - \frac{3}{4}} \right) + f\left( { - \frac{1}{4}} \right) + f\left( {\frac{1}{4}} \right) + f\left( {\frac{3}{4}} \right) + f\left( {\frac{5}{4}} \right) + f\left( {\frac{7}{4}} \right)} \right]\\ & = \require{bbox} \bbox[2pt,border:1px solid black]{{3.70700857}}\end{align*}\]b Trapezoid Rule Show Solution
From the Midpoint Rule work we know that the width of each subinterval is \(\Delta x = \frac{1}{2}\) and for reference purposes the sketch of the graph along with the endpoints of each subinterval marked by the dots is shown below.

So, to use the Trapezoid Rule to approximate the value of the integral all we need to do is plug into the formula. Doing this gives,
\[\begin{align*}\int_{{ - 1}}^{2}{{\sqrt {{{\bf{e}}^{ - \,{x^{\,2}}}} + 1} \,dx}} & \approx \left( {\frac{{{\scriptstyle{}^{1}/{}_{2}}}}{2}} \right)\left[ {f\left( { - 1} \right) + 2f\left( { - \frac{1}{2}} \right) + 2f\left( 0 \right) + 2f\left( {\frac{1}{2}} \right) + 2f\left( 1 \right) + 2f\left( {\frac{3}{2}} \right) + f\left( 2 \right)} \right]\\ & = \require{bbox} \bbox[2pt,border:1px solid black]{{3.69596543}}\end{align*}\]c Simpson's Rule Show Solution
From the Midpoint Rule work we know that the width of each subinterval is \(\Delta x = \frac{1}{2}\) and for reference purposes the sketch of the graph along with the endpoints of each subinterval marked by the dots is shown below.

As with the first two parts all we need to do is plug into the formula to use Simpson’s Rule to approximate value of the integral. Doing this gives,
\[\begin{align*}\int_{{ - 1}}^{2}{{\sqrt {{{\bf{e}}^{ - \,{x^{\,2}}}} + 1} \,dx}} & \approx \left( {\frac{{{\scriptstyle{}^{1}/{}_{2}}}}{3}} \right)\left[ {f\left( { - 1} \right) + 4f\left( { - \frac{1}{2}} \right) + 2f\left( 0 \right) + 4f\left( {\frac{1}{2}} \right) + 2f\left( 1 \right) + 4f\left( {\frac{3}{2}} \right) + f\left( 2 \right)} \right]\\ & = \require{bbox} \bbox[2pt,border:1px solid black]{{3.70358145}}\end{align*}\]