Section 8.3 : Center Of Mass
3. Find the center of mass for the triangle with vertices \((0, 0)\), \((-4, 2)\) and \((0,6)\).
Show All Steps Hide All Steps
Start SolutionLet’s start out with a quick sketch of the region, with the center of mass indicated by the dot (the coordinates of this dot are of course to be determined in the final step…..).
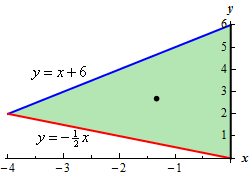
We’ll leave it to you verify the equations of the upper and lower leg of the triangle.
We’ll also need the area of this region so let’s find that first.
\[A = \int_{{ - 4}}^{0}{{\left( {x + 6} \right) - \left( { - \frac{1}{2}x} \right)\,dx}} = \int_{{ - 4}}^{0}{{\frac{3}{2}x + 6\,dx}} = \left. {\left( {\frac{3}{4}{x^2} + 6x} \right)} \right|_{ - 4}^0 = 12\] Show Step 2Next, we need to compute the two moments. We didn’t include the density in the computations below because it will only cancel out in the final step.
\[\begin{align*}{M_x} & = \int_{{ - 4}}^{0}{{\frac{1}{2}\left[ {{{\left( {x + 6} \right)}^2} - {{\left( { - \frac{1}{2}x} \right)}^2}} \right]\,dx}} = \int_{{ - 4}}^{0}{{\frac{3}{8}{x^2} + 6x + 18\,dx}} = \left. {\left( {\frac{1}{8}{x^3} + 3{x^2} + 18x} \right)} \right|_{ - 4}^0 = 32\\ {M_y} & = \int_{{ - 4}}^{0}{{x\left( {\left( {x + 6} \right) - \left( { - \frac{1}{2}x} \right)} \right)\,dx}} = \int_{{ - 4}}^{0}{{\frac{3}{2}{x^2} + 6x\,dx}} = \left. {\left( {\frac{1}{2}{x^3} + 3{x^2}} \right)} \right|_{ - 4}^0 = - 16\end{align*}\] Show Step 3Finally, the coordinates of the center of mass is,
\[\overline{x} = \frac{{{M_y}}}{M} = \frac{{\rho \left( { - 16} \right)}}{{\rho \left( {12} \right)}} = - \frac{4}{3}\hspace{0.25in}\hspace{0.25in}\overline{y} = \frac{{{M_x}}}{M} = \frac{{\rho \left( {32} \right)}}{{\rho \left( {12} \right)}} = \frac{8}{3}\]The center of mass is then : \(\require{bbox} \bbox[2pt,border:1px solid black]{{\left( { - \frac{4}{3},\frac{8}{3}} \right)}}\).