Section 9.1 : Parametric Equations and Curves
10.The path of a particle is given by the following set of parametric equations. Completely describe the path of the particle. To completely describe the path of the particle you will need to provide the following information.
- A sketch of the parametric curve (including direction of motion) based on the equation you get by eliminating the parameter.
- Limits on \(x\) and \(y\).
- A range of \(t\)’s for a single trace of the parametric curve.
- The number of traces of the curve the particle makes if an overall range of \(t\)’s is provided in the problem.
Show All Steps Hide All Steps
Start SolutionThere’s a lot of information we’ll need to find to fully answer this problem. However, for most of it we can follow the same basic ordering of steps we used for the first few problems in this section. We will need however to do a little extra work along the way.
Also, because most of the work here is similar to the work we did in Problems 4 – 6 of this section we won’t be putting in as much explanation to a lot of the work we’re doing here. So, if you need some explanation for some of the work you should go back to those problems and check the corresponding steps.
First, we’ll eliminate the parameter from this set of parametric equations. For this particular set of parametric equations let’s first notice that we can solve the \(x\) equation for the exponential function as follows,
\[{{\bf{e}}^t} = \frac{1}{2}x\]Now, just recall that \({{\bf{e}}^{3t}} = {\left( {{{\bf{e}}^t}} \right)^3}\) and so we can plug the above equation into the exponential in the \(y\) equation to get,
\[y = \cos \left( {1 + {{\bf{e}}^{3t}}} \right) = \cos \left( {1 + {{\left( {{{\bf{e}}^t}} \right)}^3}} \right) = \cos \left( {1 + {{\left( {\frac{1}{2}x} \right)}^3}} \right) = \cos \left( {1 + \frac{1}{8}{x^3}} \right)\]So, the parametric curve will be some or all of the graph of this cosine function.
Show Step 2At this point let’s work on the limits for \(x\) and \(y\). In this case, unlike most of the previous problems, things will work a little differently.
Let’s start by noting that unlike sine and cosine functions we know \({{\bf{e}}^t}\) is always an increasing function (you can do some quick Calculus I work to verify this right?).
Why do we care about this? Well first the \(x\) equation is just a constant times \({{\bf{e}}^t}\) and we are given a range of \(t\)’s for the problem. Next, the fact that \({{\bf{e}}^t}\) is an increasing function means that the \(x\) equation, \(x = 2{{\bf{e}}^t}\), is also an increasing function (because the 2 is positive). Therefore, the smallest value of \(x\) will occur at the smallest value of \(t\) in the range of \(t\)’s. Likewise, the largest value of \[x\] will occur at the largest value of \(t\) in the range of \(t\)’s.
Therefore, the range of \(x\) for our parametric curve is,
\[2{{\bf{e}}^0} \le x \le 2{{\bf{e}}^{\frac{3}{4}}}\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}2 \le x \le 2{{\bf{e}}^{\frac{3}{4}}}\]Unlike the previous problems where we usually needed to do a little more verification work we know at this point that this is the range of \(x\)’s.
For the range of \(y\)’s we will need to do a little work to get the correct range of \(y\)’s but it won’t be as much extra work as in previous problems and we can do it all in this step. First let’s notice that because the \(y\) equation is in the form of \(y = \cos \left( \cdots \right)\). The argument of the cosine doesn’t matter for the first part of the work and so wasn’t included here.
From the behavior of cosine we then know that the largest possible range of \(y\) would then be,
\[ - 1 \le y \le 1\]Now, depending on just what values the argument of the cosine in the \(y\) equation takes over the give range of \(t\)’s we may or may not cover this full range of values. We could do some work analyzing the argument of the cosine to figure that out if it does cover this full range. However, there is a really easy way to figure that if the full range is covered in this case.
Let’s just sketch the graph and see what we get. Here is a quick sketch of the graph.
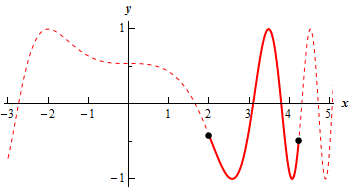
Given the “messy” nature of the argument of the cosine it’s probably best to use some form of computational aid to get the graph. The dotted portion of the graph is full graph of the function on \( - 3 \le x \le 5\) without regards to the actual restriction on \(t\). The solid portion of the graph is the portion that corresponds to the range of \(t\)’s we were given in the problem.
From this graph we can see that the range of \(y\)’s is in fact \( - 1 \le y \le 1\).
Before proceeding with the direction of motion let’s note that we could also have just graphed the curve in many of the previous problems to determine if the work in this step was the actual range or not. We didn’t do that because we could determine if these ranges were correct or not when we did the direction of motion and range of \(t\)’s for one trace analysis (which we had to do anyway) and so didn’t need to bother with a graph in this step for those problems.
Show Step 3We now need to do the direction of motion for this curve but note that we actually found the direction of motion in the previous step.
As noted in the previous step we know that \(x = 2{{\bf{e}}^t}\) is an increasing function and so the \(x\)’s must be increasing as \(t\) increases. Therefore, the equation must be moving from left to right as the curve is traced out over the given range of \(t\)’s.
Also note that unlike the previous problems we know that no portion of the graph will be retraced. Again, we know the \(x\) equation is an increasing equation. If the curve were to retrace any portion we can see that the only way to do that would be to move back from right to left which would require \(x\) to decrease and that can’t happen.
This means that we now know as well that the graph will trace out exactly once for the given range of \(t\)’s, which in turn tells us that the given range of \(t\)’s is also the range of \(t\)’s for a single trace.
Show Step 4Now that we have all the needed information we can do a formal sketch of the graph.
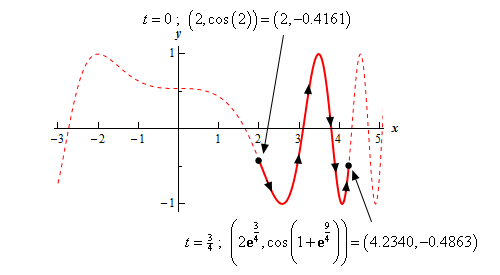
As with the graph above the dotted portion of the graph is full graph of the function on \( - 3 \le t \le 5\) without regards to the actual restriction on \(t\). The solid portion of the graph is the portion that corresponds to the range of \(t\)’s we were given in the problem. We also included the \(t\) value and coordinates of each end point for clarity although these are often not required for many problems.
Here is also the formal answers for all the rest of the information that problem asked for.
\[\begin{array}{lcc}{\mbox{Range of }}x{\mbox{ :}} & \hspace{0.1in} & 2 \le x \le 2{{\bf{e}}^{\frac{3}{4}}}\\ {\mbox{Range of }}y{\mbox{ :}} & \hspace{0.1in} & - 1 \le y \le 1\\ {\mbox{Range of }}t{\mbox{ for one trace : }} & \hspace{0.1in}& 0 \le t \le \frac{3}{4}\,\,\\ {\mbox{Total number of traces : }} & \hspace{0.1in} & 1\end{array}\]