Section 9.1 : Parametric Equations and Curves
2. Eliminate the parameter for the following set of parametric equations, sketch the graph of the parametric curve and give any limits that might exist on \(x\) and \(y\).
\[x = 4 - 2t\hspace{0.5in}y = 3 + 6t - 4{t^2}\hspace{0.25in}0 \le t \le 3\]Show All Steps Hide All Steps
Start SolutionBefore we get started on this problem we should acknowledge that this problem is really just a restriction on the first problem (i.e. it is the same problem except we restricted the values of \(t\) to use). As such we could just go back to the first problem and modify the sketch to match the restricted values of \(t\) to get a quick solution and in general that is how a problem like this would work.
However, we’re going to approach this solution as if this was its own problem because we won’t always have the more general problem worked ahead of time. So, let’s proceed with the problem assuming we haven’t worked the first problem in this section.
First, we’ll eliminate the parameter from this set of parametric equations. For this particular set of parametric equations we can do that by solving the \(x\) equation for \(t\) and plugging that into the \(y\) equation.
Doing that gives (we’ll leave it to you to verify all the algebra bits…),
\[t = \frac{1}{2}\left( {4 - x} \right)\hspace{0.5in}\,\, \to \hspace{0.5in}\,\,\,y = 3 + 6\left[ {\frac{1}{2}\left( {4 - x} \right)} \right] - 4{\left[ {\frac{1}{2}\left( {4 - x} \right)} \right]^2} = - {x^2} + 5x - 1\] Show Step 2Okay, from this it looks like we have a parabola that opens downward. To sketch the graph of this we’ll need the \(x\)-intercepts, \(y\)-intercept and most importantly the vertex.
For notational purposes let’s define \(f\left( x \right) = - {x^2} + 5x - 1\).
The \(x\)-intercepts are then found by solving \(f\left( x \right) = 0\). Doing this gives,
\[ - {x^2} + 5x - 1 = 0\hspace{0.5in}\,\,\,\, \to \hspace{0.5in}\,\,\,x = \frac{{ - 5 \pm \sqrt {{{\left( 5 \right)}^2} - 4\left( { - 1} \right)\left( { - 1} \right)} }}{{2\left( { - 1} \right)}} = \frac{{5 \pm \sqrt {21} }}{2} = 0.2087,\,\,\,4.7913\]The \(y\)-intercept is : \(\left( {0,f\left( 0 \right)} \right) = \left( {0, - 1} \right)\).
Finally, the vertex is,
\[\left( { - \frac{b}{{2a}},f\left( { - \frac{b}{{2a}}} \right)} \right) = \left( {\frac{{ - 5}}{{2\left( { - 1} \right)}},f\left( {\frac{5}{2}} \right)} \right) = \left( {\frac{5}{2},\frac{{21}}{4}} \right)\] Show Step 3Before we sketch the graph of the parametric curve recall that all parametric curves have a direction of motion, i.e. the direction indicating increasing values of the parameter, \(t\) in this case.
There are several ways to get the direction of motion for the curve. One is to plug in values of \(t\) into the parametric equations to get some points that we can use to identify the direction of motion.
Here is a table of values for this set of parametric equations. Also note that because we’ve restricted the value of \(t\) for this problem we need to keep that in mind as we chose values of \(t\) to use.
| \(t\) | \(x\) | \(y\) |
|---|---|---|
| 0 | 4 | 3 |
| \(\frac{3}{4}\) | \(\frac{5}{2}\) | \(\frac{{21}}{4}\) |
| 1 | 2 | 5 |
| 2 | 0 | -1 |
| 3 | -2 | -15 |
Note that \(t = \frac{3}{4}\) is the value of \(t\) that give the vertex of the parabola and is not an obvious value of \(t\) to use! In fact, this is a good example of why just using values of \(t\) to sketch the graph is such a bad way of getting the sketch of a parametric curve. It is often very difficult to determine a good set of \(t\)’s to use.
For this table we first found the vertex \(t\) by using the fact that we actually knew the coordinates of the vertex (the \(x\)-coordinate for this example was the important one) as follows,
\[x = \frac{5}{2}\,\,\,\,:\,\,\,\,\,\frac{5}{2} = 4 - 2t\hspace{0.5in} \to \hspace{0.5in}\,\,t = \frac{3}{4}\]Once this value of \(t\) was found we chose several values of \(t\) to either side for a good representation of \(t\) for our sketch.
Note that, for this case, we used the \(x\)-coordinates to find the value of the \(t\) that corresponds to the vertex because this equation was a linear equation and there would be only one solution for \(t\). Had we used the \(y\)‑coordinate we would have had to solve a quadratic (not hard to do of course) that would have resulted in two \(t\)’s. The problem is that only one \(t\) gives the vertex for this problem and so we’d need to then check them in the \(x\) equation to determine the correct one. So, in this case we might as well just go with the \(x\) equation from the start.
Also note that there is an easier way (probably – it will depend on you of course) to determine direction of motion. Take a quick look at the \(x\) equation.
\[x = 4 - 2t\]Because of the minus sign in front of the \(t\) we can see that as \(t\) increases \(x\) must decrease (we can verify with a quick derivative/Calculus I analysis if we want to). This means that the graph must be tracing out from right to left as the table of values above in the table also indicates.
Using a quick Calculus analysis of one, or both, of the parametric equations is often a better and easier method for determining the direction of motion for a parametric curve. For “simple” parametric equations we can often get the direction based on a quick glance at the parametric equations and it avoids having to pick “nice” values of \(t\) for a table.
Show Step 4Let’s now get the limits on \(x\) and \(y\) and note that we really do need these before we start sketching the curve!
In this case we have a parabola that opens downward and we could use that to get a general set of limits on \(x\) and \(y\). However, for this problem we’ve also restricted the values of \(t\) that we’re using and that will in turn restrict the values of \(x\) and \(y\) that we can use for the sketch of the graph.
As we discussed above we know that the graph will sketch out from right to left and so the rightmost value of \(x\) will come from \(t = 0\), which is \(x = 4\). Likewise, the leftmost value of \(y\) will come from \(t = 3\), which is \(x = - 2\). So, from this we can see the limits on \(x\) must be \( - 2 \le x \le 4\).
For the limits on the \(y\) we’ve got be a little more careful. First, we know that the vertex occurs in the given range of \(t\)’s and because the parabola opens downward the largest value of \(y\) we will have is \(y = \frac{{21}}{4}\), i.e. the \(y\)-coordinate of the vertex. Also, because the parabola opens downward we know that the smallest value of \(y\) will have to be at one of the endpoints. So, for \(t = 0\) we have \(y = 3\) and for \(t = 3\) we have \(y = - 15\). Therefore, the limits on \(y\) must be \( - 15 \le y \le \frac{{21}}{4}\).
So, putting all this together here are the limits on \(x\) and \(y\).
\[ - 2 < x < 4\hspace{0.25in}\hspace{0.25in} - 15 \le y \le \frac{{21}}{4}\]Note that for this problem we must have these limits prior to the sketching step. Because we’ve restricted the values of \(t\) to use we will have limits on \(x\) and \(y\) (as we just discussed) and so we will only have a portion of the graph of the full parabola. Having these limits will allow us to get the sketch of the parametric curve.
Show Step 5Finally, here is a sketch of the parametric curve for this set of parametric equations.
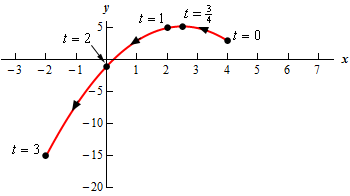
For this sketch we included the points from our table because we had them but we won’t always include them as we are often only interested in the sketch itself and the direction of motion.
Also note that it is vitally important that we not extend the graph past the \(t = 0\) and \(t = 3\) points. If we extend the graph past these points we are implying that the graph will extend past them and of course it doesn’t!