It looks like we’ll need to the following trig substitution.

\[x - 2 = \frac{1}{3}\tan \left( \theta \right)\]

Next let’s eliminate the root.

\[\sqrt {9{{\left( {x - 2} \right)}^2} + 1} = \sqrt {\tan {{\left( \theta \right)}^2} + 1} = \sqrt {{{\sec }^2}\left( \theta \right)} = \left| {\sec \left( \theta \right)} \right|\]

Next, because we are doing an indefinite integral we will assume that the secant is positive and so we can drop the absolute value bars to get,

\[\sqrt {9{{\left( {x - 2} \right)}^2} + 1} = \sec \left( \theta \right)\]

For a final substitution preparation step let’s also compute the differential so we don’t forget to use that in the substitution!

\[\left( 1 \right)dx = \frac{1}{3}{\sec ^2}\left( \theta \right)\,d\theta \hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}dx = \frac{1}{3}{\sec ^2}\left( \theta \right)\,d\theta \]

Recall that all we really need to do here is compute the differential for both the right and left sides of the substitution.

Show Step 3

Now let’s do the actual substitution.

\[\int{{\frac{1}{{\sqrt {9{x^2} - 36x + 37} }}\,dx}} = \int{{\frac{1}{{\sec \left( \theta \right)}}\left( {\frac{1}{3}{{\sec }^2}\left( \theta \right)} \right)\,d\theta }} = \frac{1}{3}\int{{\sec \left( \theta \right)\,d\theta }}\]

Do not forget to substitute in the differential we computed in the previous step. This is probably the most common mistake with trig substitutions. Forgetting the differential can substantially change the problem, often making the integral very difficult to evaluate.

Show Step 4

We now need to evaluate the integral. Here is that work.

\[\int{{\frac{1}{{\sqrt {9{x^2} - 36x + 37} }}\,dx}} = \frac{1}{3}\ln \left| {\sec \left( \theta \right) + \tan \left( \theta \right)} \right| + c\]

Note that this was one of the few trig substitution integrals that didn’t really require a lot of manipulation of trig functions to completely evaluate. All we had to really do here was use the fact that we determined the integral of \(\sec \left( \theta \right)\) in the previous section and reuse that result here.

Show Step 5

As the final step we just need to go back to \(x\)’s. To do this we’ll need a quick right triangle. Here is that work.

From the substitution we have, \[\tan \left( \theta \right) = \frac{{3\left( {x - 2} \right)}}{1}\,\,\,\,\,\left( { = \frac{{{\mbox{opp}}}}{{{\mbox{adj}}}}} \right)\] From the right triangle we get, \[\sec \left( \theta \right) = \sqrt {9{{\left( {x - 2} \right)}^2} + 1} \]

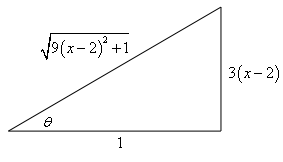
The integral is then,

\[\int{{\frac{1}{{\sqrt {9{x^2} - 36x + 37} }}\,dx}} = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{1}{3}\ln \left| {\sqrt {9{{\left( {x - 2} \right)}^2} + 1} + 3\left( {x - 2} \right)} \right| + c}}\]