Let’s first use the substitution to eliminate the root.

\[\sqrt {{x^2} + 16} = \sqrt {16{{\tan }^2}\left( \theta \right) + 16} = 4\sqrt {{{\sec }^2}\left( \theta \right)} = 4\left| {\sec \left( \theta \right)} \right|\]

Next, because we are doing an indefinite integral we will assume that the secant is positive and so we can drop the absolute value bars to get,

\[\sqrt {{x^2} + 16} = 4\sec \left( \theta \right)\]

For a final substitution preparation step let’s also compute the differential so we don’t forget to use that in the substitution!

\[dx = 4{\sec ^2}\left( \theta \right)\,d\theta \] Show Step 3

Now let’s do the actual substitution.

\[\int{{\frac{{\sqrt {{x^2} + 16} }}{{{x^4}}}\,dx}} = \int{{\frac{{4\sec \left( \theta \right)}}{{{{\left( {4\tan \left( \theta \right)} \right)}^4}}}\,4{{\sec }^2}\left( \theta \right)d\theta }} = \int{{\frac{{{{\sec }^3}\left( \theta \right)}}{{16{{\tan }^4}\left( \theta \right)}}\,d\theta }}\]

Do not forget to substitute in the differential we computed in the previous step. This is probably the most common mistake with trig substitutions. Forgetting the differential can substantially change the problem, often making the integral very difficult to evaluate.

Show Step 4

We now need to evaluate the integral. In this case the integral looks to be a little difficult to do in terms of secants and tangents so let’s convert the integrand to sines and cosines and see what we get. Doing this gives,

\[\int{{\frac{{\sqrt {{x^2} + 16} }}{{{x^4}}}\,dx}} = \frac{1}{{16}}\int{{\frac{{\cos \left( \theta \right)}}{{{{\sin }^4}\left( \theta \right)}}\,d\theta }}\]

This is a simple integral to evaluate so here is the integral evaluation.

\[\begin{align*}\int{{\frac{{\sqrt {{x^2} + 16} }}{{{x^4}}}\,dx}} & = \frac{1}{{16}}\int{{\frac{{\cos \left( \theta \right)}}{{{{\sin }^4}\left( \theta \right)}}\,d\theta }}\hspace{0.25in}\hspace{0.25in}u = \sin \left( \theta \right)\\ & = \frac{1}{{16}}\int{{{u^{ - 4}}\,du}}\\ & = - \frac{1}{{48}}{u^{ - 3}} + c = - \frac{1}{{48}}{\left[ {\sin \left( \theta \right)} \right]^{ - 3}} + c = - \frac{1}{{48}}{\csc ^3}\left( \theta \right) + c\end{align*}\]

Don’t forget all the “standard” manipulations of the integrand that we often need to do in order to evaluate integrals involving trig functions. If you don’t recall them you’ll need to go back to the previous section and work some practice problems to get good at them.

Every trig substitution problem reduces down to an integral involving trig functions and the majority of them will need some manipulation of the integrand in order to evaluate.

Show Step 5

As the final step we just need to go back to \(x\)’s. To do this we’ll need a quick right triangle. Here is that work.

From the substitution we have, \[\tan \left( \theta \right) = \frac{x}{4}\,\,\,\,\,\left( { = \frac{{{\mbox{opp}}}}{{{\mbox{adj}}}}} \right)\] From the right triangle we get, \[\csc \left( \theta \right) = \frac{{\sqrt {{x^2} + 16} }}{x}\]

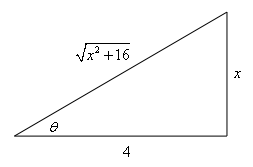
The integral is then,

\[\int{{\frac{{\sqrt {{x^2} + 16} }}{{{x^4}}}\,dx}} = - \frac{1}{{48}}{\left[ {\frac{{\sqrt {{x^2} + 16} }}{x}} \right]^3} + c = \require{bbox} \bbox[2pt,border:1px solid black]{{ - \frac{{{{\left( {{x^2} + 16} \right)}^{\frac{3}{2}}}}}{{48{x^3}}} + c}}\]