Section 16.6 : Conservative Vector Fields
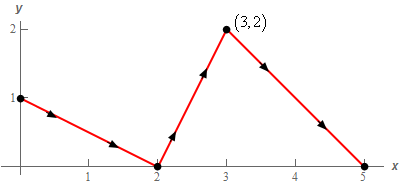
9. Evaluate \( \displaystyle \int\limits_{C}{{\vec F\centerdot d\vec r}}\) where \(\vec F\left( {x,y} \right) = \left( {2y{{\bf{e}}^{x\,y}} + 2x{{\bf{e}}^{{x^{\,2}} - {y^{\,2}}}}} \right)\,\vec i + \left( {2x{{\bf{e}}^{x\,y}} - 2y{{\bf{e}}^{{x^{\,2}} - {y^{\,2}}}}} \right)\vec j\) and \(C\) is the curve shown below.
Show All Steps Hide All Steps
Start SolutionThere are two ways to work this problem, a hard way and an easy way. The hard way is to just see a line integral with a curve and a vector field given and just launch into computing the line integral directly (probably quite unpleasant in this case). The easy way is to check and see if the vector field is conservative, and if it is find the potential function and then simply use the Fundamental Theorem for Line Integrals that we saw in the previous section.
So, let’s go the easy way and check to see if the vector field is conservative.
\[\begin{align*}P & = 2y{{\bf{e}}^{x\,y}} + 2x{{\bf{e}}^{{x^{\,2}} - {y^{\,2}}}}&\hspace{0.25in}{P_y} & = 2{{\bf{e}}^{x\,y}} + 2xy{{\bf{e}}^{x\,y}} - 4xy{{\bf{e}}^{{x^{\,2}} - {y^{\,2}}}}\\ Q & = 2x{{\bf{e}}^{x\,y}} - 2y{{\bf{e}}^{{x^{\,2}} - {y^{\,2}}}} & \hspace{0.25in}{Q_x} & = 2{{\bf{e}}^{x\,y}} + 2xy{{\bf{e}}^{x\,y}} - 4xy{{\bf{e}}^{{x^{\,2}} - {y^{\,2}}}}\end{align*}\]So, we can see that \({P_y} = {Q_x}\) and so the vector field is conservative.
Show Step 2Now we just need to find the potential function for the vector field. We’ll go through those details a little quicker this time and with less explanation than we did in the some of the previous problems.
First, let’s integrate \(Q\) with respect to \(y\).
\[\begin{align*}f\left( {x,y} \right) & = \int{{Q\,dy}}\\ & = \int{{2x{{\bf{e}}^{x\,y}} - 2y{{\bf{e}}^{{x^{\,2}} - {y^{\,2}}}}\,dy}}\\ & = 2{{\bf{e}}^{x\,y}} + {{\bf{e}}^{{x^{\,2}} - {y^{\,2}}}} + g\left( x \right)\end{align*}\]Now, differentiate with respect to \(x\) and set equal to \(P\).
\[{f_x} = 2y{{\bf{e}}^{x\,y}} + 2x{{\bf{e}}^{{x^{\,2}} - {y^{\,2}}}} + g'\left( x \right) = 2y{{\bf{e}}^{x\,y}} + 2x{{\bf{e}}^{{x^{\,2}} - {y^{\,2}}}} = P\hspace{0.25in} \Rightarrow \,\,\,\,\,\,\,\,g'\left( x \right) = 0\]Solving for \(g\left( x \right)\) gives \(g\left( x \right) = c\) and so the potential function for this vector field is,
\[f\left( {x,y} \right) = 2{{\bf{e}}^{x\,y}} + {{\bf{e}}^{{x^{\,2}} - {y^{\,2}}}} + c\] Show Step 3Now that we have the potential function we can simply use the Fundamental Theorem for Line Integrals which says,
\[ \displaystyle \int\limits_{C}{{\vec F\centerdot d\vec r}} = f\left( {{\mbox{end point}}} \right) - f\left( {{\mbox{start point}}} \right)\]From the graph in the problem statement we can see that the starting point of \(C\) is \(\left( {0,1} \right)\) and the ending point of \(C\) is \(\left( {5,0} \right)\).
The integral is then,
\[\int\limits_{C}{{\vec F\centerdot d\vec r}} = f\left( {5,0} \right) - f\left( {0,1} \right) = \left( {2 + {{\bf{e}}^{25}} + c} \right) - \left( {2 + {{\bf{e}}^{ - 1}} + c} \right) = \require{bbox} \bbox[2pt,border:1px solid black]{{{{\bf{e}}^{25}} - {{\bf{e}}^{ - 1}}}}\]