Calculus III - Double Integrals over General Regions

Hide Mobile Notice

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 15.3 : Double Integrals over General Regions

Back to Problem List

5. Evaluate $\displaystyle \iint\limits_{D}{{5{x^3}\cos \left( {{y^3}} \right)\,dA}}$ where $D$ is the region bounded by $y = 2$ , $\displaystyle y = \frac{1}{4}{x^2}$ and the $y$ -axis.

Show All Steps Hide All Steps

Start Solution

Below is a quick sketch of the region $D$ .

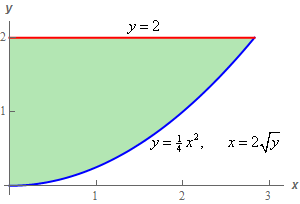
Note that we gave both forms of the equation for the lower curve to help with the next step.

In general, this sketch is often important to setting the integral up correctly. We’ll need to determine the order of integration and often the region will “force” a particular order. Many regions can only be dealt with easily by doing one particular order of integration and sometimes the only way to really see that is to have a sketch of $D$ .

Even if you can do the integral in either order the sketch of $D$ will often help with setting up the limits for the integrals.

Show Step 2

With this problem the region can be dealt with either order of integration. The integral on the other hand can’t. We simply cannot integrate $y$ first as there is no ${y^2}$ in front of the cosine we’d need to do the substitution. So, we’ll have no choice but to do the $x$ integration first.

So, here are the limits for this integral.

$\begin{array}{c}0 \le y \le 2\\ 0 \le x \le 2\sqrt y \end{array}$ Show Step 3

Here is the integral set up for $x$ integration first.

$\iint\limits_{D}{{5{x^3}\cos \left( {{y^3}} \right)\,dA}} = \int_{0}^{2}{{\int_{0}^{{2\sqrt y }}{{5{x^3}\cos \left( {{y^3}} \right)\,dx}}\,dy}}$ Show Step 4

Here is the $x$ integration.

$\begin{align*}\iint\limits_{D}{{5{x^3}\cos \left( {{y^3}} \right)\,dA}} & = \int_{0}^{2}{{\int_{0}^{{2\sqrt y }}{{5{x^3}\cos \left( {{y^3}} \right)\,dx}}\,dy}}\\ & = \int_{0}^{2}{{\left. {\left( {\frac{5}{4}{x^4}\cos \left( {{y^3}} \right)} \right)} \right|_0^{2\sqrt y }\,dy}}\\ & = \int_{0}^{2}{{20{y^2}\cos \left( {{y^3}} \right)\,dy}}\end{align*}$ Show Step 5

Note that while we couldn’t do the $y$ integration first we can do it now. The ${y^2}$ we need for the substitution is now there after doing the $x$ integration.

Here is the $y$ integration.

$\begin{align*}\iint\limits_{D}{{5{x^3}\cos \left( {{y^3}} \right)\,dA}} & = \int_{0}^{2}{{20{y^2}\cos \left( {{y^3}} \right)\,dy}}\\ & = \left. {\left( {\frac{{20}}{3}\sin \left( {{y^3}} \right)} \right)} \right|_0^2 = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{20}}{3}\sin \left( 8 \right) = 6.5957}}\end{align*}$

Remember to have your calculator set to radians when computing to decimals.