Calculus III - Double Integrals in Polar Coordinates

Hide Mobile Notice

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 15.4 : Double Integrals in Polar Coordinates

Back to Problem List

1. Evaluate $\displaystyle \iint\limits_{D}{{{y^2} + 3x\,dA}}$ where $D$ is the region in the 3^rd quadrant between ${x^2} + {y^2} = 1$ and ${x^2} + {y^2} = 9$ .

Show All Steps Hide All Steps

Start Solution

Below is a quick sketch of the region $D$ .

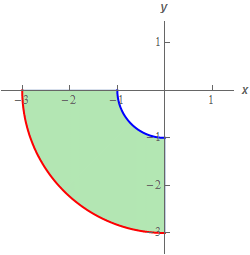
For double integrals in which polar coordinates are going to be used the sketch of $D$ is often not as useful as for a general region.

However, if nothing else, it does make it clear that polar coordinates will be needed for this problem. Describing this region in terms of Cartesian coordinates is possible but it would take two integrals to do the problem and the most of the limits will involve roots which often (not always, but often) leads to messy integral work.

The sketch shows that the region is at least partially circular and that should always indicate that polar coordinates are not a bad thing to at least think about. In this case, because of the Cartesian limits as discussed above polar coordinates are pretty much the only easy way to do this integral.

Note as well that once we have the sketch determining the polar limits should be pretty simple.

Show Step 2

Okay, $D$ is just a portion of a ring and so setting up the limits shouldn’t be too difficult. Here they are,

$\begin{array}{c}\pi \le \theta \le \frac{3}{2}\pi \\ \,1 \le r \le 3\end{array}$ Show Step 3

The integral in terms of polar coordinates is then,

$\begin{align*}\iint\limits_{D}{{{y^2} + 3x\,dA}} & = \int_{\pi }^{{\frac{3}{2}\pi }}{{\int_{1}^{3}{{\left( {{{\left( {r\sin \theta } \right)}^2} + 3r\cos \theta } \right)r\,dr}}\,d\theta }}\\ & = \int_{\pi }^{{\frac{3}{2}\pi }}{{\int_{1}^{3}{{{r^3}{{\sin }^2}\theta + 3{r^2}\cos \theta \,dr}}\,d\theta }}\end{align*}$

When converting the integral don’t forget to convert the $x$ and $y$ into polar coordinates. Also, don’t forget that $dA = r\,dr\,d\theta$ and so we’ll pickup an extra $r$ in the integrand. Forgetting the extra $r$ is one of the most common mistakes with these kinds of problems.

Show Step 4

Here is the $r$ integration.

$\begin{align*}\iint\limits_{D}{{{y^2} + 3x\,dA}} & = \int_{\pi }^{{\frac{3}{2}\pi }}{{\int_{1}^{3}{{{r^3}{{\sin }^2}\theta + 3{r^2}\cos \theta \,dr}}\,d\theta }}\\ & = \int_{\pi }^{{\frac{3}{2}\pi }}{{\left. {\left( {\frac{1}{4}{r^4}{{\sin }^2}\theta + {r^3}\cos \theta } \right)} \right|_1^3\,d\theta }}\\ & = \int_{\pi }^{{\frac{3}{2}\pi }}{{20{{\sin }^2}\theta + 26\cos \theta \,d\theta }}\end{align*}$ Show Step 5

Finally, here is the $\theta$ integration.

$\begin{align*}\iint\limits_{D}{{{y^2} + 3x\,dA}} & = \int_{\pi }^{{\frac{3}{2}\pi }}{{20{{\sin }^2}\theta + 26\cos \theta \,d\theta }}\\ & = \int_{\pi }^{{\frac{3}{2}\pi }}{{10\left( {1 - \cos \left( {2\theta } \right)} \right) + 26\cos \theta \,d\theta }}\\ & = \left. {\left( {10\theta - 5\sin \left( {2\theta } \right) + 26\sin \theta } \right)} \right|_\pi ^{\frac{3}{2}\pi } = \require{bbox} \bbox[2pt,border:1px solid black]{{5\pi - 26}}\end{align*}$

You’ll be seeing a fair amount of ${\cos ^2}\theta$ , ${\sin ^2}\theta$ and $\sin \theta \cos \theta$ terms in polar integrals so make sure that you know how to integrate these terms! In this case we used a half angle formula to reduce the ${\sin ^2}\theta$ into something we could integrate.