Section 16.2 : Line Integrals - Part I
2. Evaluate \( \displaystyle \int\limits_{C}{{2y{x^2} - 4x\,ds}}\) where \(C\) is the lower half of the circle centered at the origin of radius 3 with clockwise rotation.
Show All Steps Hide All Steps
Start SolutionHere is a quick sketch of \(C\) with the direction specified in the problem statement shown.
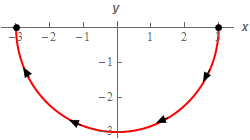
Here is a parameterization for this curve.
\[\vec r\left( t \right) = \left\langle {3\cos \left( t \right), - 3\sin \left( t \right)} \right\rangle \,\,\,\,\,\,\,\,0 \le t \le \pi \]We could also break this up into parameter form as follows.
\[\begin{array}{*{20}{l}}{x = 3\cos \left( t \right)}\\{y = - 3\sin \left( t \right)}\end{array}\hspace{0.25in}0 \le t \le \pi \]Either form of the parameterization will work for the problem but we’ll use the vector form for the rest of this problem.
Show Step 3We’ll need the magnitude of the derivative of the parameterization so let’s get that.
\[\begin{align*}\vec r'\left( t \right) & = \left\langle { - 3\sin \left( t \right), - 3\cos \left( t \right)} \right\rangle \\ \left\| {\vec r'\left( t \right)} \right\| &= \sqrt {{{\left( { - 3\sin \left( t \right)} \right)}^2} + {{\left( { - 3\cos \left( t \right)} \right)}^2}} \\ & = \sqrt {9{{\sin }^2}\left( t \right) + 9{{\cos }^2}\left( t \right)} = \sqrt {9\left( {{{\sin }^2}\left( t \right) + {{\cos }^2}\left( t \right)} \right)} = \sqrt 9 = 3\end{align*}\]We’ll also need the integrand “evaluated” at the parameterization. Recall all this means is we replace the \(x\)/\(y\) in the integrand with the \(x\)/\(y\) from parameterization. Here is the integrand evaluated at the parameterization.
\[2y{x^2} - 4x = 2\left( { - 3\sin \left( t \right)} \right){\left( {3\cos \left( t \right)} \right)^2} - 4\left( {3\cos \left( t \right)} \right) = - 54\sin \left( t \right){\cos ^2}\left( t \right) - 12\cos \left( t \right)\] Show Step 4The line integral is then,
\[\begin{align*}\int\limits_{C}{{2y{x^2} - 4x\,ds}} & = \int_{0}^{\pi }{{\left( { - 54\sin \left( t \right){{\cos }^2}\left( t \right) - 12\cos \left( t \right)} \right)3\,dt}}\\ & = 3\left. {\left[ {18{{\cos }^3}\left( t \right) - 12\sin \left( t \right)} \right]} \right|_0^\pi = \require{bbox} \bbox[2pt,border:1px solid black]{{ - 108}}\end{align*}\]