Section 16.2 : Line Integrals - Part I
8. Evaluate \( \displaystyle \int\limits_{C}{{{y^3} - {x^2}\,ds}}\) for each of the following curves.
- \(C\) is the line segment from \(\left( {3,6} \right)\) to \(\left( {0,0} \right)\) followed by the line segment from \(\left( {0,0} \right)\) to \(\left( {3, - 6} \right)\).
- \(C\) is the line segment from \(\left( {3,6} \right)\) to \(\left( {3, - 6} \right)\).
Start Solution
Let’s start off with a quick sketch of the curve for this part of the problem.
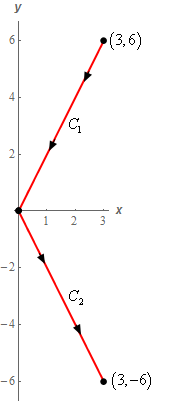
So, this curve comes in two pieces and we’ll need to parameterize each of them so let’s take care of that next.
\({C_1}:\,\,\vec r\left( t \right) = \left( {1 - t} \right)\left\langle {3,6} \right\rangle + t\left\langle {0,0} \right\rangle = \left\langle {3 - 3t,6 - 6t} \right\rangle \hspace{0.25in}\,\,\,\,\,\,\,0 \le t \le 1\)\({C_2}:\,\,\vec r\left( t \right) = \left( {1 - t} \right)\left\langle {0,0} \right\rangle + t\left\langle {3, - 6} \right\rangle = \left\langle {3t, - 6t} \right\rangle \hspace{0.25in}\,\,\,\,\,\,\,0 \le t \le 1\)
For each of these curves we just used the vector form of the line segment between two points. In the first case we needed to because the direction was in the decreasing \(y\) direction and recall that the integral limits need to be from smaller to larger value. In the second case the equation would have been just as easy to use but we just decided to use the line segment form for the slightly nicer limits.
Show Step 2Okay, we now need to compute the line integral along each of these curves. Unlike the first few problems in this section where we found the magnitude and the integrand prior to the integration step we’re just going to just straight into the integral and do all the work there.
Here is the integral along each of the curves.
\[\begin{align*}\int\limits_{{{C_1}}}{{{y^3} - {x^2}\,ds}} &= \int_{0}^{1}{{\left[ {{{\left( {6 - 6t} \right)}^3} - {{\left( {3 - 3t} \right)}^2}} \right]\sqrt {{{\left( { - 3} \right)}^2} + {{\left( { - 6} \right)}^2}} \,dt}}\\ & = \sqrt {45} \int_{0}^{1}{{{{\left( {6 - 6t} \right)}^3} - {{\left( {3 - 3t} \right)}^2}\,dt}}\\ & = \left. {3\sqrt 5 \left( { - \frac{1}{{24}}{{\left( {6 - 6t} \right)}^4} + \frac{1}{9}{{\left( {3 - 3t} \right)}^3}} \right)} \right|_0^1 = \underline {153\sqrt 5 } \end{align*}\] \[\begin{align*}\int\limits_{{{C_2}}}{{{y^3} - {x^2}\,ds}} &= \int_{0}^{1}{{\left[ {{{\left( { - 6t} \right)}^3} - {{\left( {3t} \right)}^2}} \right]\sqrt {{{\left( 3 \right)}^2} + {{\left( { - 6} \right)}^2}} \,dt}}\\ & = \sqrt {45} \int_{0}^{1}{{ - 216{t^3} - 9{t^2}\,dt}}\\ & = \left. {3\sqrt 5 \left( { - 54{t^4} - 3{t^3}} \right)} \right|_0^1 = \underline { - 171\sqrt 5 } \end{align*}\] Show Step 3Okay to finish this problem out all we need to do is add up the line integrals over these curves to get the full line integral.
\[\int\limits_{C}{{{y^3} - {x^2}\,ds}} = \left( {153\sqrt 5 } \right) + \left( { - 171\sqrt 5 } \right) = \require{bbox} \bbox[2pt,border:1px solid black]{{ - 18\sqrt 5 }}\]Note that we put parenthesis around the result of each individual line integral simply to illustrate where it came from and they aren’t needed in general of course.
b \(C\) is the line segment from \(\left( {3,6} \right)\) to \(\left( {3, - 6} \right)\). Show All Steps Hide All Steps
Start Solution
Let’s start off with a quick sketch of the curve for this part of the problem.
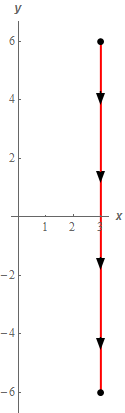
So, what we have in this part is a different curve that goes from \(\left( {3,6} \right)\) to \(\left( {3, - 6} \right)\). Despite the fact that this curve has the same starting and ending point as the curve in the first part there is no reason to expect the line integral to have the same value. Therefore we’ll need to go through the work and see what we get from the line integral.
We’ll need to parameterize the curve so let’s take care of that.
\(C:\,\,\vec r\left( t \right) = \left( {1 - t} \right)\left\langle {3,6} \right\rangle + t\left\langle {3, - 6} \right\rangle = \left\langle {3,6 - 12t} \right\rangle \hspace{0.25in}\,\,\,\,\,\,\,0 \le t \le 1\)Because this curve is in the direction of decreasing \(y\) and the integral needs its limits to go from smaller to larger values we had to use the vector form of the line segment between two points.
Show Step 2Now all we need to do is compute the line integral.
\[\begin{align*}\int\limits_{C}{{{y^3} - {x^2}\,ds}} & = \int_{0}^{1}{{\left[ {{{\left( {6 - 12t} \right)}^3} - {{\left( 3 \right)}^2}} \right]\sqrt {{{\left( 0 \right)}^2} + {{\left( { - 12} \right)}^2}} \,dt}}\\ & = 12\int_{0}^{1}{{{{\left( {6 - 12t} \right)}^3} - 9\,dt}}\\ & = \left. {12\left( { - \frac{1}{{48}}{{\left( {6 - 12t} \right)}^4} - 9t} \right)} \right|_0^1 = \require{bbox} \bbox[2pt,border:1px solid black]{{ - 108}}\end{align*}\]So, as noted at the start of this part the value of the line integral was not the same as the value of the line integral in the first part despite the same starting and ending points for the curve. Note that it is possible for two line integrals with the same starting and ending points to have the same value but we can’t expect that to happen and so need to go through and do the work.