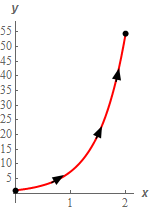
Next, we need to parameterize the curve.

\[\vec r\left( t \right) = \left\langle {t,{{\bf{e}}^{2t}}} \right\rangle \hspace{0.25in}0 \le t \le 2\] Show Step 3

Now we need to evaluate the line integral. Be careful with this type line integral. Note that the differential, in this case, is \(dy\) and not \(ds\) as they were in the previous section.

All we need to do is recall that \(dy = y'\,dt\) when we convert the line integral into a “standard” integral.

So, let’s evaluate the line integral. Just remember to “plug in” the parameterization into the integrand (i.e. replace the \(x\) and \(y\) in the integrand with the \(x\) and \(y\) components of the parameterization) and to convert the differential properly.

Here is the line integral.

\[\begin{align*}\int\limits_{C}{{\sqrt {1 + y} \,dy}} &= \int_{0}^{2}{{\sqrt {1 + {{\bf{e}}^{2t}}} \,\,\left( {2{{\bf{e}}^{2t}}} \right)\,dt}}\\ & = \left. {\left[ {\frac{2}{3}{{\left( {1 + {{\bf{e}}^{2t}}} \right)}^{\frac{3}{2}}}} \right]} \right|_0^2 = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{2}{3}\left[ {{{\left( {1 + {{\bf{e}}^4}} \right)}^{\frac{3}{2}}} - {2^{\frac{3}{2}}}} \right] = 274.4897}}\end{align*}\]

Note that, in this case, the integral ended up being a simple substitution.