Section 16.3 : Line Integrals - Part II
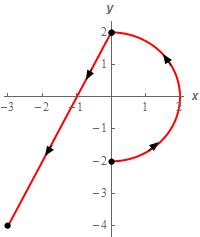
4. Evaluate \( \displaystyle \int\limits_{C}{{1 + {x^3}\,dx}}\) where \(C\) is the right half of the circle of radius 2 with counter clockwise rotation followed by the line segment from \(\left( {0,2} \right)\) to \(\left( { - 3, - 4} \right)\). See the sketch below for the direction.
Show All Steps Hide All Steps
Start SolutionTo help with the problem let’s label each of the curves as follows,
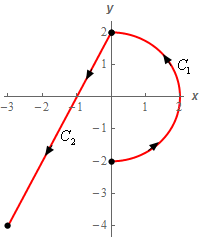
Now let’s parameterize each of these curves.
\({C_1}:\,\,\vec r\left( t \right) = \left\langle {2\cos \left( t \right),2\sin \left( t \right)} \right\rangle \hspace{0.25in} - \frac{1}{2}\pi \le t \le \frac{1}{2}\pi \)\({C_2}:\,\,\vec r\left( t \right) = \left( {1 - t} \right)\left\langle {0,2} \right\rangle + t\left\langle { - 3, - 4} \right\rangle = \left\langle { - 3t,2 - 6t} \right\rangle \hspace{0.25in}0 \le t \le 1\)
Show Step 2
Now we need to compute the line integral for each of the curves.
\[\begin{align*}\int\limits_{{{C_1}}}{{1 + {x^3}\,dx}} & = \int_{{ - \,\,\frac{1}{2}\pi }}^{{\frac{1}{2}\pi }}{{\left[ {1 + {{\left( {2\cos \left( t \right)} \right)}^3}} \right]\left( { - 2\sin \left( t \right)} \right)\,dt}}\\ & = \int_{{ - \,\,\frac{1}{2}\pi }}^{{\frac{1}{2}\pi }}{{ - 2\sin \left( t \right) - 16{{\cos }^3}\left( t \right)\sin \left( t \right)\,dt}}\\ & = \left. {\left( {2\cos \left( t \right) + 4{{\cos }^4}\left( t \right)} \right)} \right|_{ - \,\frac{1}{2}\pi }^{\frac{1}{2}\pi } = \underline 0 \end{align*}\] \[\begin{align*}\int\limits_{{{C_2}}}{{1 + {x^3}\,dx}} & = \int_{0}^{1}{{\left[ {1 + {{\left( { - 3t} \right)}^3}} \right]\left( { - 3} \right)\,dt}}\\ & = \int_{0}^{1}{{ - 3 + 81{t^3}\,dt}}\\ & = \left. {\left( { - 3t + \frac{{81}}{4}{t^4}} \right)} \right|_0^1 = \underline {\frac{{69}}{4}} \end{align*}\]Don’t forget to correctly deal with the differentials when converting the line integral into a “standard” integral.
Show Step 3Okay to finish this problem out all we need to do is add up the line integrals over these curves to get the full line integral.
\[ \displaystyle \int\limits_{C}{{1 + {x^3}\,dx}} = \left( 0 \right) + \left( {\frac{{69}}{4}} \right) = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{69}}{4}}}\]Note that we put parenthesis around the result of each individual line integral simply to illustrate where it came from and they aren’t needed in general of course.