Section 16.4 : Line Integrals of Vector Fields
8. Evaluate \( \displaystyle \int\limits_{C}{{\vec F\centerdot d\vec r}}\) where \(\vec F\left( {x,y} \right) = 3\,\vec i + \left( {xy - 2x} \right)\vec j\) for each of the following curves.
- \(C\) is the upper half of the circle centered at the origin of radius 4 with counter clockwise rotation.
- \(C\) is the upper half of the circle centered at the origin of radius 4 with clockwise rotation.
Start Solution
Let’s start off with a quick sketch of the curve for this part of the problem.
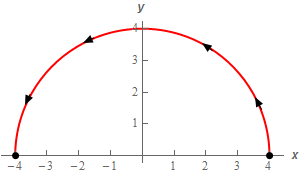
For reasons that will become apparent once we get to the second part of this problem let’s call this curve \({C_1}\) instead of \(C\). Here then is the parameterization of \({C_1}\).
\({C_1}:\,\,\vec r\left( t \right) = \left\langle {4\cos \left( t \right),4\sin \left( t \right)} \right\rangle \hspace{0.25in}\,\,\,\,\,\,\,0 \le t \le \pi \)Show Step 2
Here is the line integral for this curve.
\[\begin{align*}\int\limits_{{{C_1}}}{{\vec F\centerdot d\vec r}} & = \int_{0}^{\pi }{{\left\langle {3,\left( {4\cos \left( t \right)} \right)\left( {4\sin \left( t \right)} \right) - 2\left( {4\cos \left( t \right)} \right)} \right\rangle \centerdot \left\langle { - 4\sin \left( t \right),4\cos \left( t \right)} \right\rangle \,dt}}\\ & = \int_{0}^{\pi }{{ - 12\sin \left( t \right) + 64\sin \left( t \right){{\cos }^2}\left( t \right) - 32{{\cos }^2}\left( t \right)\,dt}}\\ & = \int_{0}^{\pi }{{ - 12\sin \left( t \right) + 64\sin \left( t \right){{\cos }^2}\left( t \right) - 16\left( {1 + \cos \left( {2t} \right)} \right)\,dt}}\\ & = \left. {\left( {12\cos \left( t \right) - \frac{{64}}{3}{{\cos }^3}\left( t \right) - 16t - 8\sin \left( {2t} \right)} \right)} \right|_0^\pi = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{56}}{3} - 16\pi = - 31.5988}}\end{align*}\]b \(C\) is the upper half of the circle centered at the origin of radius 4 with clockwise rotation. Show All Steps Hide All Steps
Start Solution
Now, as we did in the previous part let’s “rename” this curve as \({C_2}\) instead of \(C\).
Next, note that this curve is just the curve from the first step with opposite direction. In other words what we have here is that \({C_2} = - {C_1}\). Here is a quick sketch of \({C_2}\) for the sake of completeness.
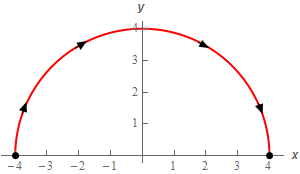
Now, at this point there are two different methods we could use to evaluate the integral.
The first method is use the fact from the notes that if we switch the direction of a curve then the value of this type of line integral will just change signs. Using this fact along with the relationship between the curve from this part and the curve from the first part, i.e. \({C_2} = - {C_1}\) , the line integral is just,
\[\int\limits_{{{C_2}}}{{\vec F\centerdot d\vec r}} = \int\limits_{{ - {C_1}}}{{\vec F\centerdot d\vec r}} = - \int\limits_{{{C_1}}}{{\vec F\centerdot d\vec r}} = \require{bbox} \bbox[2pt,border:1px solid black]{{16\pi - \frac{{56}}{3} = 31.5988}}\]Note that the first equal sign above was just acknowledging the relationship between the two curves. The second equal sign is where we used the fact from the notes.
This is the “easy” method for doing this problem. Alternatively, we could parameterize up the curve and compute the line integral directly. We will do that for the rest of this problem just to show how we would go about doing that.
Show Step 3Here is the parameterization for this curve.
\({C_2}:\,\,\vec r\left( t \right) = \left\langle { - 4\cos \left( t \right),4\sin \left( t \right)} \right\rangle \hspace{0.25in}\,\,\,\,\,\,\,0 \le t \le \pi \)Show Step 4
Now all we need to do is compute the line integral.
\[\begin{align*}\int\limits_{{{C_2}}}{{\vec F\centerdot d\vec r}} & = \int_{0}^{\pi }{{\left\langle {3,\left( { - 4\cos \left( t \right)} \right)\left( {4\sin \left( t \right)} \right) - 2\left( { - 4\cos \left( t \right)} \right)} \right\rangle \centerdot \left\langle {4\sin \left( t \right),4\cos \left( t \right)} \right\rangle \,dt}}\\ & = \int_{0}^{\pi }{{12\sin \left( t \right) - 64\sin \left( t \right){{\cos }^2}\left( t \right) + 32{{\cos }^2}\left( t \right)\,dt}}\\ & = \int_{0}^{\pi }{{12\sin \left( t \right) - 64\sin \left( t \right){{\cos }^2}\left( t \right) + 16\left( {1 + \cos \left( {2t} \right)} \right)\,dt}}\\ & = \left. {\left( { - 12\cos \left( t \right) + \frac{{64}}{3}{{\cos }^3}\left( t \right) + 16t + 8\sin \left( {2t} \right)} \right)} \right|_0^\pi = \require{bbox} \bbox[2pt,border:1px solid black]{{16\pi - \frac{{56}}{3} = 31.5988}}\end{align*}\]So, the line integral from this part had the same value, except for the sign, as the line integral from the first part as we expected it to.